Sign In

JEE Advance - Physics (2010 - Paper 1 Offline - No. 21)

When a particle of mass m moves on the x-axis in a potential of the form V(x) = kx2, it performs simple harmonic motion. The corresponding time period is proportional to $$\sqrt {{m \over k}} $$, as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = $$\alpha$$x4 ($$\alpha$$ > 0) for | x | near the origin and becomes a constant equal to V0 for (see figure).

When a particle of mass m moves on the x-axis in a potential of the form V(x) = kx2, it performs simple harmonic motion. The corresponding time period is proportional to $$\sqrt {{m \over k}} $$, as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = $$\alpha$$x4 ($$\alpha$$ > 0) for | x | near the origin and becomes a constant equal to V0 for (see figure).

When a particle of mass m moves on the x-axis in a potential of the form V(x) = kx2, it performs simple harmonic motion. The corresponding time period is proportional to $$\sqrt {{m \over k}} $$, as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x) = $$\alpha$$x4 ($$\alpha$$ > 0) for | x | near the origin and becomes a constant equal to V0 for (see figure).

If the total energy of the particle is E, it will perform periodic motion only if
E < 0
E > 0
V0 > E > 0
E > V0

Explanation

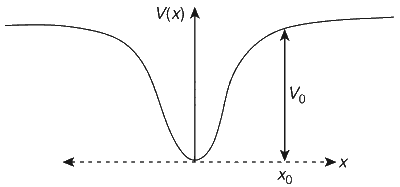
The kinetic energy of the particle cannot be negative. The total energy E is the sum of the kinetic energy K(x) and potential energy V(x) i.e.,

E = K(x) + V(x). ....... (1)

IIT-JEE 2010 Paper 1 Offline Physics - Simple Harmonic Motion Question 12 English Explanation

From the given figure, V(x) $$\ge$$ 0 for all x. If E $$\le$$ 0 for some x then kinetic energy K(x) = E $$-$$ V(x) $$\le$$ 0 for those x and hence the motion of the particle is not allowed for those x. On the other hand, if E $$\ge$$ V0 then K(x) = E $$-$$ V(x) $$\ge$$ 0 for all x and particle is allowed to move for all x, including infinity (in this case the particle will escape to infinity). Thus, for the particle to have a periodic motion, V0 > E > 0. In this case, particle is allowed at points where

K(x) = E $$-$$ V(x) = E $$-$$ $$\alpha$$x4 $$\ge$$ 0 i.e.,

| x | $$\le$$ (E/$$\alpha$$)1/4.

Comments (0)

Advertisement