JEE Advance - Physics (2010 - Paper 1 Offline - No. 2)
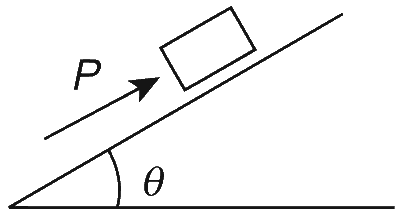
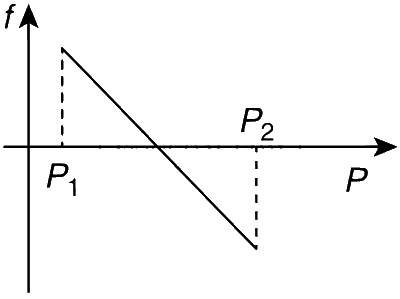
A block of mass m is on an inclined plane of angle θ. The coefficient of friction between the block and the plane is μ and tan θ > μ. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from P1 = mg(sinθ − μ cosθ) to P2 = mg(sinθ + μ cosθ), the frictional force f versus P graph will look like
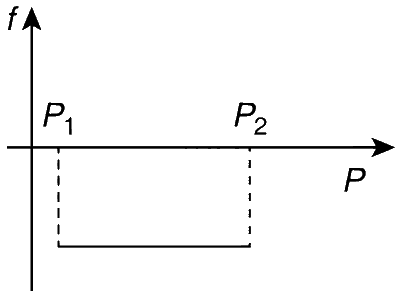
Explanation
The forces acting on the block are its weight mg, normal reaction N, applied force P and frictional force f.
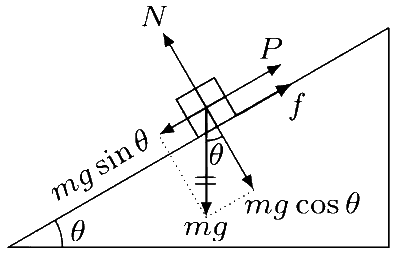
Resolve mg along and normal to the inclined plane and apply Newton's second law to get
$$0 = P + f - mg\sin \theta $$,
which gives
$$f = - P + mg\sin \theta $$. ...... (1)
This is a straight line with slope $$-$$1. Substitute the values of P1 and P2 in equation (1) to get the frictional force at those points i.e.,
$${f_1} = \mu mg\cos \theta $$ and $${f_2} = - \mu mg\cos \theta $$.
Comments (0)


