JEE Advance - Physics (2010 - Paper 1 Offline - No. 18)
A ray OP of monochromatic light is incident on the face AB of prism ABCD near vertex B at an incident angle of 60$$^\circ$$ (see figure). If the refractive index of the material of the prism is $$\sqrt3$$, which of the following is(are) correct?
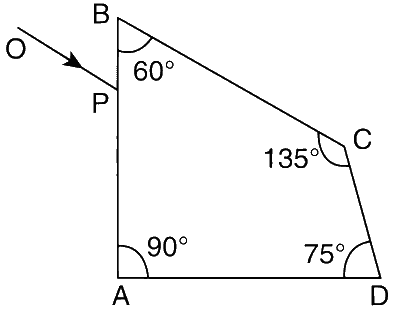
Explanation
Consider the refraction at the face AB. Snell's law,
$$\sin i/\sin r = \sin 60^\circ /\sin r = \sqrt 3 $$,
gives $$r = 30^\circ $$.
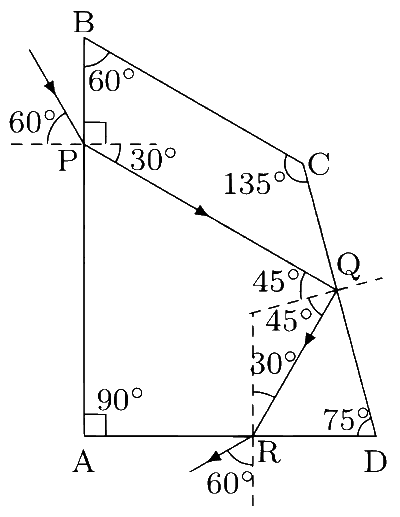
The geometry in BCQP gives
$$\angle BPQ = 30^\circ + 90^\circ = 120^\circ $$
$$\angle CQP = 360^\circ - (135^\circ + 60^\circ + 120^\circ ) = 45^\circ $$.
Thus, the angle of incidence at Q is $${i_1} = 45^\circ $$. The critical angle for prism to air refraction is given by $$\sin {i_c} = 1/\sqrt 3 $$. Since $$\sin {i_1} = 1/\sqrt 2 > 1\sqrt 3 $$, we get $${i_1} > {i_c}$$ i.e., the angle of incidence is greater than the critical angle. Thus, the ray undergoes total internal reflection at Q. The laws of reflection gives $${r_1} = {i_1} = 45^\circ $$. In triangle QRD, $$\angle QRD = 60^\circ $$ and hence the angle of incidence at R is $${i_2} = 30^\circ $$.
Applying Snell's law at face AD, we get
$$\sqrt 3 \times \sin 30^\circ = 1 \times \sin e$$
or, $$\sqrt 3 \times {1 \over 2} = \sin e$$
$$\sin e = {{\sqrt 3 } \over 2}$$
or, $$e = {\sin ^{ - 1}}\left( {{{\sqrt 3 } \over 2}} \right) = 60^\circ $$
From figure,
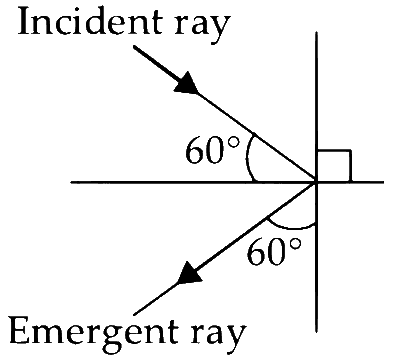
The angle between the incident ray and the emergent ray is 90$$^\circ$$.
Hence, option (c) is correct and option (d) is incorrect.
Note : Angle between incident and emergent rays is the same as the angle between the two faces = 90$$^\circ$$.
Comments (0)


