JEE Advance - Physics (2010 - Paper 1 Offline - No. 15)
A thin uniform annular disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass from point P on its axis to infinity is
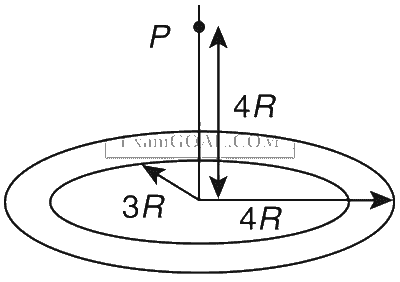
Explanation
We need to find gravitational potential energy of a unit mass placed at the point P.
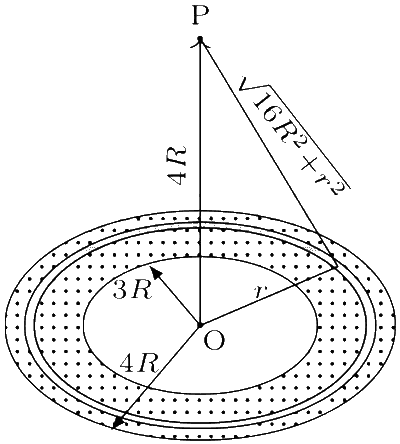
The surface mass density of the annular disc is
$$\sigma = M/(16\pi {R^2} - 9\pi {R^2}) = M/(7\pi {R^2})$$.
Consider a small ring of radius r and thickness dr. The mass of the ring is dm = 2$$\pi$$r$$\sigma $$dr. As distance of any point of the ring from P is same, the potential at P due to the ring is
$${V_P} = - {{G(2\pi r\sigma dr)} \over {\sqrt {16{R^2} + {r^2}} }}$$
Integrate from r = 3R to r = 4R to get the potential energy of the unit mass placed at P
$${V_P} = \int\limits_{3R}^{4R} { - {{GdM} \over {\sqrt {{{(4R)}^2} + {{(r)}^2}} }} = - {{GM2\pi } \over {7\pi {R^2}}}\int\limits_{3R}^{4R} {{{rdr} \over {\sqrt {16{R^2} + {r^2}} }}} } $$
Solving, we get
$${V_P} = - {{GM2\pi } \over {7\pi {R^2}}}\left[ {\sqrt {16{R^2} + {r^2}} } \right]_{3R}^{4R} = - {{2GM} \over {7R}}\left( {4\sqrt 2 - 5} \right)$$
Work done in moving a unit mass from P to $$\infty$$ = V$$\infty$$ $$-$$VP
$$ = 0 - \left( {{{ - 2GM} \over {7R}}\left( {4\sqrt 2 - 5} \right)} \right) = {{2GM} \over {7R}}\left( {4\sqrt 2 - 5} \right)$$
Comments (0)


