JEE Advance - Physics (2010 - Paper 1 Offline - No. 1)
A 0.1 kg mass is suspended from a wire of negligible mass. The length of the wire is 1 m and its crosssectional area is 4.9 $$ \times $$ 10-7 m2. If the mass is pulled a little in the vertically downward direction and released, it performs simple harmonic motion of angular frequency 140 rad s−1. If the Young’s modulus of the material of the wire is n $$ \times $$ 109 Nm-2, the value of n is
Answer
4
Explanation
When mass m is pulled by a force F, the wire elongation x, length l, cross-sectional area A, and Young's modulus of wire material Y are related by $$Y = {{F/A} \over {x/l}}$$ i.e.,
$$F = (Y\,A/l)x$$.
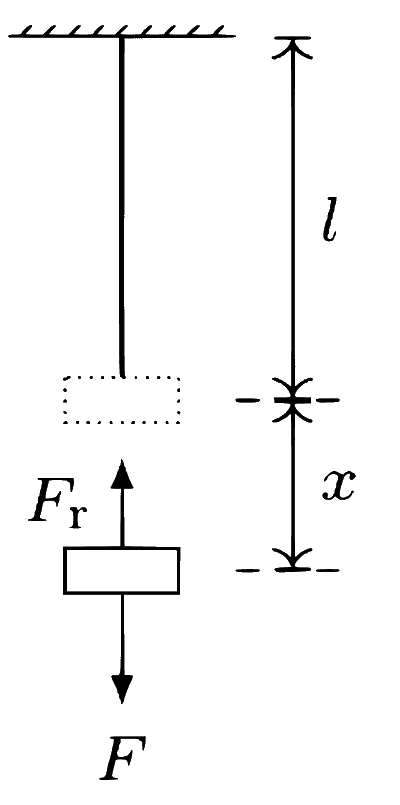
The restoring force by the wire is equal but opposite to F i.e., Fr = $$-$$F. Apply Newton's second law to get
$$m{d^2}x/d{t^2} = - (YA/l)x = - {\omega ^2}x$$.
This equation represents SHM with an angular frequency $$\omega = \sqrt {YA/(lm)} $$. Substitute the values to get $$Y = {\omega ^2}lm/A = 4 \times {10^9}$$ N/m2.
Comments (0)


