JEE Advance - Physics (2009 - Paper 2 Offline - No. 8)
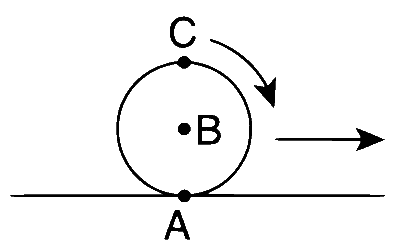
A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure below, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then,
Explanation
We have
$$\overrightarrow {{V_C}} = \overrightarrow {{V_{CM}}} + \overrightarrow {r\omega } = 2\overrightarrow {{V_{CM}}} $$
$$\overrightarrow {{V_B}} = \overrightarrow {{V_{CM}}} $$
$$\overrightarrow {{V_A}} = 0$$
Therefore,
$$\overrightarrow {{V_C}} - \overrightarrow {{V_B}} = \overrightarrow {r\omega } = \overrightarrow {{V_{CM}}} $$
$$\overrightarrow {{V_B}} - \overrightarrow {{V_A}} = \overrightarrow {{V_{CM}}} $$
$$\overrightarrow {{V_C}} - \overrightarrow {{V_A}} = \overrightarrow {{V_{CM}}} + \overrightarrow {r\omega } = 2\overrightarrow {{V_{CM}}} $$
$$\overrightarrow {{V_B}} - \overrightarrow {{V_C}} = - \overrightarrow {r\omega } $$
For pure rolling, we have
$$|\overrightarrow {{V_{CM}}} | = |\overrightarrow {r\omega } |$$
Therefore,
$$|\overrightarrow {{V_C}} - \overrightarrow {{V_A}} | = 2{V_{CM}}$$
$$ \Rightarrow 2|\overrightarrow {{V_B}} - \overrightarrow {{V_C}} | = 2r\omega = 2{V_{CM}}$$
Comments (0)


