JEE Advance - Physics (2009 - Paper 2 Offline - No. 4)
A uniform rod of length L and mass M is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $$k$$. The springs are fixed to rigid supports as shown in the figure, and the rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle $$\theta$$ in one direction and released. The frequency of oscillation is
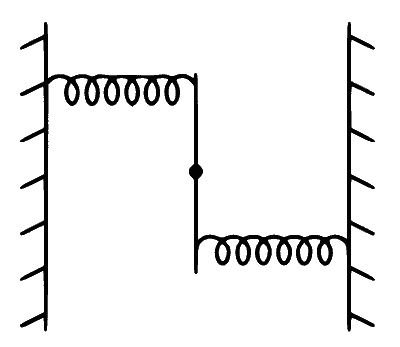
Explanation
The restoring torque is
$$J = - 2 \times kx\left( {{L \over 2}} \right)\cos \theta = I\left( {{{{d^2}\theta } \over {d{t^2}}}} \right)$$
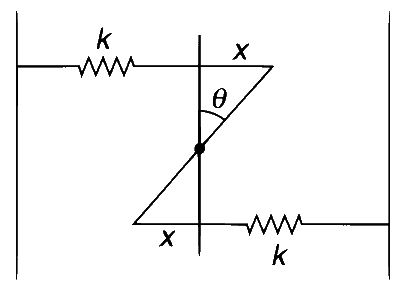
Now, $$x = {L \over 2}\sin \theta $$
Therefore, $$J = - k\left( {{{{L^2}} \over 2}} \right)\sin \theta \cos \theta = I\left( {{{{d^2}\theta } \over {d{t^2}}}} \right)$$
$$ \Rightarrow \left( {{{ - k{L^2}} \over 4}} \right)\sin 2\theta = I\left( {{{{d^2}\theta } \over {d{t^2}}}} \right)$$
For small $$\theta$$, $$\sin 2\theta = 2\theta $$. Therefore,
$${{ - k{L^2}\theta } \over 2} = I\left( {{{{d^2}\theta } \over {d{t^2}}}} \right)$$
where $$I = {{M{L^2}} \over {12}}$$. Therefore,
$${{{d^2}\theta } \over {d{t^2}}} = \left( {{{ - 6k} \over M}} \right)\theta = - {\omega ^2}\theta $$ (SHM)
$$ \Rightarrow \omega = \sqrt {{{6k} \over M}} $$
Hence, the frequency of oscillation is
$${\omega \over {2\pi }} = {1 \over {2\pi }}\sqrt {{{6k} \over M}} $$
Comments (0)


