JEE Advance - Physics (2009 - Paper 2 Offline - No. 18)
A metal rod AB of length 10x has its one end A in ice at 0$$^\circ$$C and the other end B in water at 100$$^\circ$$C. If a point P on the rod is maintained at 400$$^\circ$$C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540 cal/g and latent heat of melting of ice is 80 cal/g. If the point P is at a distance of $$\lambda x$$ from the ice end A, find the value of $$\lambda$$. (Neglect any heat loss to the surrounding.)
Answer
9
Explanation
The steady rate of flow of heat is
$${{\Delta Q} \over {\Delta t}} = kA\left( {{{\Delta T} \over {\Delta x}}} \right)$$
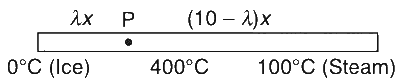
Therefore, $${{kA(400 - 0^\circ )} \over {\lambda x}} = {m_{ice}}\,{l_{ice}}$$
$${{kA(400 - 100)} \over {(10 - \lambda )x}} = {m_{water}}\,{l_{water}}$$
where $${m_{ice}}$$ is the mass of ice melted per unit times and $${m_{water}}$$ is the mass of water evaporated per unit times. It is given that
$${m_{ice}} = {m_{water}}$$
Therefore, $${{kA \times 400} \over {\lambda x({l_{ice}})}} = {{kA \times 300} \over {(10 - \lambda )x\,{l_{water}}}}$$
$$ \Rightarrow 4(10 - \lambda ) \times 540 = 3\lambda \times 80$$
$$ \Rightarrow 5400 - 540\lambda = 60\lambda $$
$$ \Rightarrow \lambda = 9$$
Comments (0)


