The segments PQ and PR, in the triangle shown here, cannot produce $$\overrightarrow B $$ at point P since point P lies on them. Here, only QR creates $$\overrightarrow B $$ at point P.

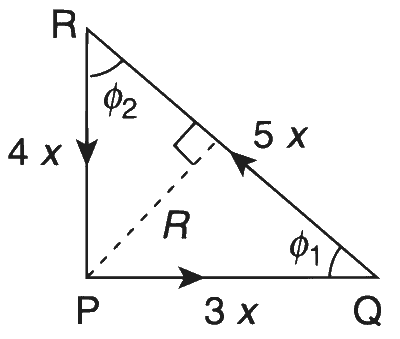
Applying $${B_P} = {{{\mu _0}i} \over {4\pi R}}(\cos {\phi _1} + \cos {\phi _2})$$, where $${\phi _1} = 53^\circ $$ and $${\phi _2} = 37^\circ $$, we get the magnitude of the magnetic field as follows:

$${B_P} = {{{\mu _0}I} \over {4\pi (4\pi \sin 37^\circ )}}(\cos 53^\circ + \cos 37^\circ )$$

$$ = {{{\mu _0}I} \over {16\pi x(3/5)}}\left( {{{3x} \over {5x}} + {{4x} \over {5x}}} \right)$$

$$ = {{5{\mu _0}I} \over {48\pi x}}\left( {{7 \over 5}} \right) = {{7{\mu _0}I} \over {48\pi x}} = k\left( {{{{\mu _0}I} \over {48\pi x}}} \right)$$

where $$k = 7$$.