JEE Advance - Physics (2009 - Paper 2 Offline - No. 13)
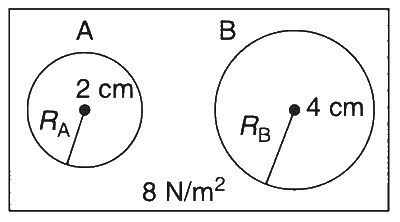
Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8 N/m$$^2$$. The radii of bubbles A and B are 2 cm and 4 cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. Find the ratio $$n_B/n_A$$, where $$n_A$$ and $$n_B$$ are the number of moles of air in bubbles A and B, respectively. (Neglect the effect of gravity.)
Answer
6
Explanation
We have,
$${P_A} = {P_0} + {{4S} \over {{r_A}}} = 8 + \left[ {{{4(0.04)} \over {2 \times {{10}^{ - 2}}}}} \right] = 16$$ N/m$$^2$$
$${P_B} = {P_0} + {{4S} \over {{r_B}}} = 9 + \left[ {{{4(0.04)} \over {4 \times {{10}^{ - 2}}}}} \right] = 12$$ N/m$$^2$$
Now, $$PV = nRT$$
Therefore, $${{{n_B}} \over {{n_A}}} = {{{P_B}{V_B}} \over {{P_A}{V_A}}} - {{{P_B}r_B^3} \over {{P_A}r_A^3}} = {{12} \over {16}} \times {{64} \over 8} = 6$$
Comments (0)


