JEE Advance - Physics (2009 - Paper 2 Offline - No. 11)
Column I shows four situations of standard Young's double slit arrangement with the screen placed far away from the slits S$$_1$$ and S$$_2$$. In each of these cases, S$$_1$$P$$_0$$ = S$$_2$$P$$_0$$, S$$_1$$P$$_1$$ $$-$$ S$$_2$$P$$_1$$ = $$\lambda/4$$ and S$$_1$$P$$_2$$ $$-$$ S$$_2$$P$$_2$$ = $$\lambda/3$$, where $$\lambda$$ is the wavelength of the light used. In the cases B, C and D, a transparent sheet of refractive index $$\mu$$ and thickness t is pasted on slit S$$_2$$. The thickness of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by $$\delta$$(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation:
| Column I | Column II | ||
|---|---|---|---|
| (A) | 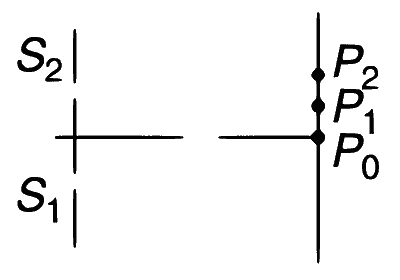 |
(P) | $$\delta ({P_0}) = 0$$ |
| (B) | $$(\mu-1)t=\lambda/4$$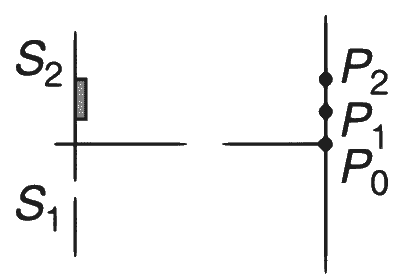 |
(Q) | $$\delta ({P_1}) = 0$$ |
| (C) | $$(\mu-1)t=\lambda/2$$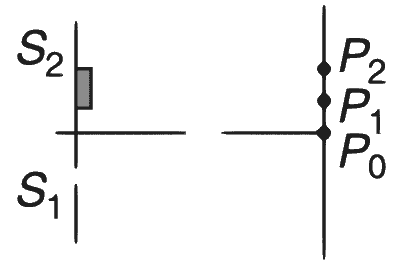 |
(R) | $$I({P_1}) = 0$$ |
| (D) | $$(\mu-1)t=3\lambda/4$$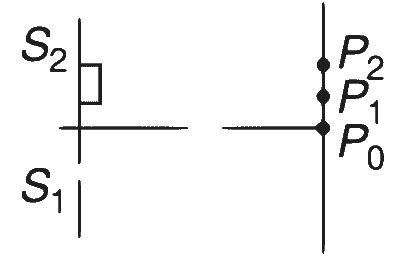 |
(S) | $$I({P_0}) > I({P_1})$$ |
| (T) | $$I({P_2}) > I({P_1})$$ |
Explanation
(A)$$\to$$(P), (S)
Since the path difference is
$$S_1P_0=S_2P_0=0$$
the phase difference becomes
$$\delta(P_0)=0$$
The intensity at any point is
$$I = {I_{\max }}{\cos ^2}\left( {{8 \over 2}} \right)$$
Now, $$I({P_0}) = {I_{\max }}$$ [$$\because$$ $$\delta ({P_0}) = 0$$]
$$I({P_1}) = {I_{\max }}{\cos ^2}\left( {{\pi \over 4}} \right) = {{{I_{\max }}} \over 2}$$
Therefore, $$I({P_0}) > I({P_1})$$
(B)$$\to$$(Q)
In this case, the path difference at P$$_1$$ is
$${P_1} = {\lambda \over 4} - (\mu - 1)t = {\lambda \over 4} - {\lambda \over 4} = 0$$
Therefore, $$\delta ({P_1}) = 0$$.
(C)$$\to$$(T)
In this case, the path difference at P$$_1$$ is
$${P_1} = {\lambda \over 4} - (\mu - 1)t = {\lambda \over 4} - {\lambda \over 2} = {{ - \lambda } \over 4}$$
Therefore, the phase difference at P$$_1$$ is
$${P_1} = {{2\pi } \over \lambda } \times \left( {{{ - \lambda } \over 4}} \right) = - {\pi \over 2}$$
Therefore, $$I({P_1}) = {I_{\max }}{\cos ^2}\left( {{\pi \over 4}} \right) = {{{I_{\max }}} \over 2}$$
The path difference at P$$_2$$ is
$${P_2} = {\lambda \over 3} - (\mu - 1)t = {\lambda \over 3} - {\lambda \over 2} = {{ - \lambda } \over 6}$$
Therefore, the phase difference at P$$_1$$ is
$${P_2} = {{2\pi } \over \lambda } \times \left( {{{ - \lambda } \over 6}} \right) = - {\pi \over 3}$$
Therefore, $$I({P_2}) = {I_{\max }}{\cos ^2}\left( {{\pi \over 6}} \right) = {3 \over 4}{I_{\max }}$$
Therefore, $$I({P_2}) > I({P_1})$$.
(D)$$\to$$(R), (S), (T)
In this case, the path difference at P$$_1$$ is
$${P_1} = {\lambda \over 4} - (\mu - 1)t = {\lambda \over 4} - {{3\lambda } \over 4} = {{ - \lambda } \over 2}$$
Therefore, the phase difference at P$$_1$$ is
$${P_1} = {{2\pi } \over \lambda } \times \left( { - {\lambda \over 2}} \right) = - \pi $$
Therefore, $$I({P_1}) = {I_{\max }}{\cos ^2}\left( {{\pi \over 2}} \right) = 0$$
The path difference at P$$_0$$ is
$${P_0} = 0 - (\mu - 1)t = {{ - 3\lambda } \over 4}$$
Therefore, the phase difference at P$$_0$$ is
$${P_0} = {{2\pi } \over \lambda } \times \left( {{{ - 3\lambda } \over 4}} \right) = {{ - 3\lambda } \over 2}$$
Therefore, $$I({P_0}) = {I_{\max }}{\cos ^2}{{3\pi } \over 4} = {{{I_{\max }}} \over 2}$$
Now, the path difference at P$$_1$$ is
$${P_1} = {\lambda \over 4} - (\mu - 1)t = {\lambda \over 4} - {{3\lambda } \over 4} = - {\lambda \over 2}$$
The phase difference at P$$_1$$ is
$${P_1} = {{2\pi } \over \lambda } \times \left( {{{ - \lambda } \over 2}} \right) = - \pi $$
Therefore, $$I({P_1}) = {I_{\max }}\cos \left( {{\pi \over 2}} \right) = 0$$
Comments (0)


