JEE Advance - Physics (2009 - Paper 2 Offline - No. 1)
A piece of wire is bent in the shape of a parabola y = kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration $$a$$. The distance of the
new equilibrium position of the bead, where the bead can stays at rest with respect to the wire, from the y-axis is
$${a \over {gk}}$$
$${a \over {2gk}}$$
$${{2a} \over {gk}}$$
$${a \over {4gk}}$$
Explanation
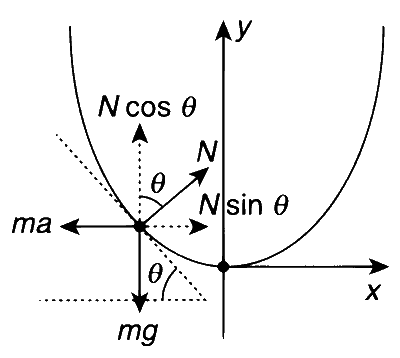
While the parabola is moving right side, the bead experiences a force with a magnitude $$ma$$ to the left. That is, at equilibrium,
$$N\cos \theta = mg$$
$$N\sin \theta = ma$$
Now, $$\tan \theta = {a \over g}$$
Also, $$\tan \theta = {{dy} \over {dx}} = 2kx \Rightarrow x = {a \over {2gk}}$$
Comments (0)


