JEE Advance - Physics (2008 - Paper 1 Offline - No. 6)
A spherically symmetric gravitational system of particles has a mass density
$$\rho = \left\{ {\matrix{ {{\rho _0}} & {for} & {r \le R} \cr 0 & {for} & {r > R} \cr } } \right.$$
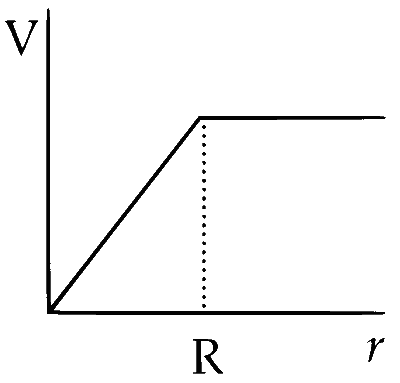
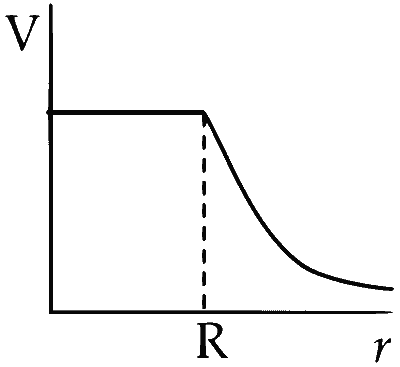
Where $$\rho_0$$ is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed V as a function of distance $$r(0 < r < \infty)$$ from the centre of the system is represented by
Explanation
For $$r\ge R$$,
Force on test mass m is $$F=m\times |E_g|$$
where, $$E_g$$ = Gravitational field intensity at the point of observation
$$\therefore$$ $${{m{v^2}} \over r} = m \times \left[ {{{GM} \over {{r^2}}}} \right]$$,
Where, M = Total mass of spherical system
$$\therefore$$ $$v \propto {1 \over {\sqrt r }}$$
For $$r < R$$,
$$F' = m|E{'_g}|$$
$$\therefore$$ $${{m{V^2}} \over r} = m\left[ {{{GM} \over {{R^3}}} \times r} \right]$$
Hence, $$V \propto r$$
Comments (0)


