Sign In

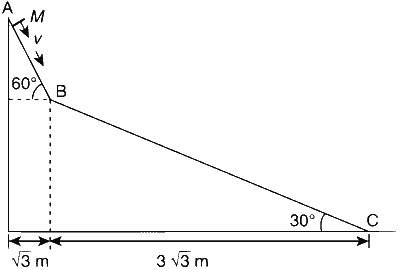
JEE Advance - Physics (2008 - Paper 1 Offline - No. 22)

A small block of mass M moves on a frictionless surface of an inclined plane, as shown in figure. The angle of the incline suddenly changes from 60$$^\circ$$ to 30$$^\circ$$ at point B. The block is initially at rest at A. Assume that collisions between the block and the incline are totally inelastic (g = 10 m/s$$^2$$).

A small block of mass M moves on a frictionless surface of an inclined plane, as shown in figure. The angle of the incline suddenly changes from 60$$^\circ$$ to 30$$^\circ$$ at point B. The block is initially at rest at A. Assume that collisions between the block and the incline are totally inelastic (g = 10 m/s$$^2$$).

A small block of mass M moves on a frictionless surface of an inclined plane, as shown in figure. The angle of the incline suddenly changes from 60$$^\circ$$ to 30$$^\circ$$ at point B. The block is initially at rest at A. Assume that collisions between the block and the incline are totally inelastic (g = 10 m/s$$^2$$).

The speed of the block at point C, immediately before it leaves the second incline is
$$\sqrt{120}$$ m/s
$$\sqrt{105}$$ m/s
$$\sqrt{90}$$ m/s
$$\sqrt{75}$$ m/s

Explanation

$$v_C^2 - v_B^2 = 2as$$

$$v_C^2 - 45 = 2 \times 10 \times 3$$

$${v_c} = \sqrt {60 + 45} = \sqrt {105} \,m{s^{ - 1}}$$ is the velocity of block just before leaving incline.

Comments (0)

Advertisement