Sign In

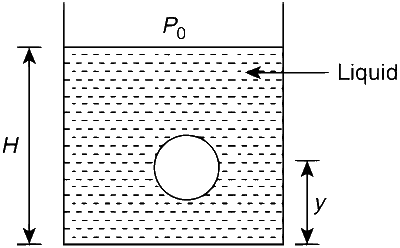
JEE Advance - Physics (2008 - Paper 1 Offline - No. 17)

A small spherical monoatomic ideal gas bubble $$\left( {\gamma = {5 \over 3}} \right)$$ is trapped inside a liquid of density $$\rho_1$$ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T$$_0$$, the height of the liquid is H and the atmospheric pressure is P$$_0$$ (Neglect surface tension)

A small spherical monoatomic ideal gas bubble $$\left( {\gamma = {5 \over 3}} \right)$$ is trapped inside a liquid of density $$\rho_1$$ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T$$_0$$, the height of the liquid is H and the atmospheric pressure is P$$_0$$ (Neglect surface tension)

A small spherical monoatomic ideal gas bubble $$\left( {\gamma = {5 \over 3}} \right)$$ is trapped inside a liquid of density $$\rho_1$$ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T$$_0$$, the height of the liquid is H and the atmospheric pressure is P$$_0$$ (Neglect surface tension)

The buoyancy force acting on the gas bubble is (Assume R is the universal gas constant)
$${\rho _l}nRg{T_0}{{{{({P_0} + {\rho _l}gH)}^{{2 \over 5}}}} \over {{{({P_0} + {\rho _l}gy)}^{{7 \over 5}}}}}$$
$${{{\rho _l}nRg{T_0}} \over {{{({P_0} + {\rho _l}gH)}^{{2 \over 5}}}{{[{P_0} + {\rho _l}g(H - y)]}^{{3 \over 5}}}}}$$
$${\rho _l}nRg{T_0}{{{{({P_0} + {\rho _l}gH)}^{{3 \over 5}}}} \over {{{({P_0} + {\rho _l}gy)}^{{8 \over 5}}}}}$$
$${{{\rho _l}nRg{T_0}} \over {{{({P_0} + {\rho _l}gH)}^{{3 \over 5}}}[{P_0} + {\rho _l}g{{(H - y)}^{{2 \over 5}}}}}$$

Explanation

Buoyancy force = Weight of fluid displaced

= (mass of fluid displaced)g

$$ = V{\rho _l}g$$ .... (i)

Where V = Volume of fluid displaced

= Volume of the bubble

$$PV = nRT$$

$$ \Rightarrow V = {{nRT} \over P} = {{nRT} \over {{P_0}(H - y){\rho _l}g}}$$ .... (ii)

Where P is the pressure of the bubble at an arbitrary location at a distance 'y' from the bottom.

Put the value of temperature from eq. (i)

$$V = {{nR} \over {[{P_0} + (H - y){\rho _l}g]}} \times {{{T_0}{{[{P_0} + (H - y){\rho _l}g]}^{2/5}}} \over {{{[{P_0} + H{\rho _l}g]}^{2/5}}}}$$

$$ = {{nR{T_0}} \over {{{[{P_0} + (H - y){\rho _l}g]}^{3/5}}{{[{P_0} + H{\rho _l}g]}^{2/5}}}}$$ .... (iii)

From eq. (i) and (iii) Buoyance force

$$ = {{nR{T_0}{\rho _1}g} \over {{{[{P_0} + (H - y){\rho _l}g]}^{3/5}}{{[{P_0} + H{\rho _l}g]}^{2/5}}}}$$

Comments (0)

Advertisement