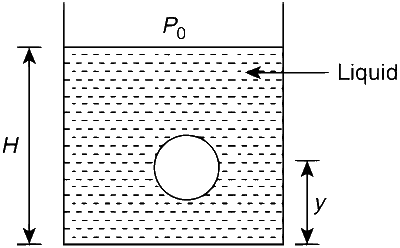
JEE Advance - Physics (2008 - Paper 1 Offline - No. 16)

A small spherical monoatomic ideal gas bubble $$\left( {\gamma = {5 \over 3}} \right)$$ is trapped inside a liquid of density $$\rho_1$$ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T$$_0$$, the height of the liquid is H and the atmospheric pressure is P$$_0$$ (Neglect surface tension)

When the gas bubble is at a height y from the bottom, its temperature is :

$${T_0}{\left( {{{{P_0} + {\rho _l}gH} \over {{P_0} + {\rho _l}gy}}} \right)^{{2 \over 5}}}$$

$${T_0}{\left( {{{{P_0} + {\rho _l}g(H - y)} \over {{P_0} + {\rho _l}gH}}} \right)^{{2 \over 5}}}$$

$${T_0}{\left( {{{{P_0} + {\rho _l}gH} \over {{P_0} + {\rho _l}gy}}} \right)^{{3 \over 5}}}$$

$${T_0}{\left( {{{{P_0} + {\rho _l}g(H - y)} \over {{P_0} + {\rho _l}gH}}} \right)^{{3 \over 5}}}$$

Explanation

Since the process is adiabatic,

$$P{V^\gamma }$$ = constant for gas inside bubble.

Thus, $$P{V^{(1 - \gamma )}}.\,{T^\gamma } = $$ constant

$$ \Rightarrow {P^{1 - \gamma }}_{bottom}{T^\gamma }_{bottom} = P_y^{1 - \gamma }T_y^\gamma = $$ constant

$$ \Rightarrow {({P_0} + {\rho _1}gH)^{ - 2/3}}(T_0^{5/3}) = ({P_0} + {\rho _1}g{(H - y)^{ - 2/3}}){T^{5/3}}$$

$$ \Rightarrow {T_0} = {\left[ {{{{P_0} + {\rho _1}g(H - y)} \over {{P_0} + {\rho _1}gH}}} \right]^{2/5}}$$

JEE Advance - Physics (2008 - Paper 1 Offline - No. 16)

Explanation

Comments (0)