Sign In

JEE Advance - Physics (2007 - Paper 2 Offline - No. 5)

Water is filled up to a height $$h$$ in a beaker of radius $$R$$ as shown in the figure. The density of water is $$\rho$$, the surface tension of water is $$T$$ and the atmospheric pressure is P. Consider a vertical section $$A B C D$$ of the water column through a diameter of the beaker. The force on water on one side of this section by water on the other side of this section has magnitude

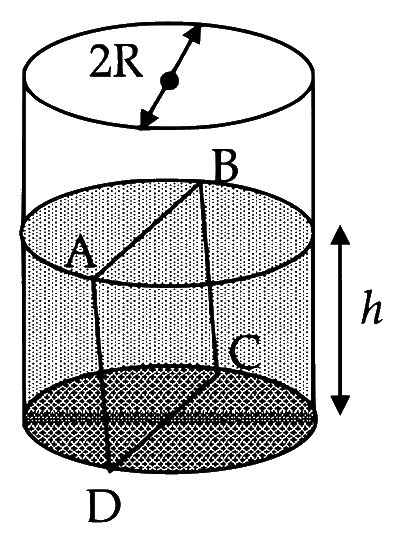
IIT-JEE 2007 Paper 2 Offline Physics - Properties of Matter Question 4 English

$$\left|2 \mathrm{P}_{0} \mathrm{Rh}+\pi \mathrm{R}^{2} \rho g h-2 \mathrm{RT}\right|$$
$$\left|2 \mathrm{P}_{0} \mathrm{Rh}+\pi \mathrm{R \rho gh}^{2}-2 \mathrm{RT}\right|$$
$$\left|P_{0} \pi R^{2}+R \rho g h^{2}-2 R T\right|$$
$$\left|\mathrm{P}_{0} \mathrm{R}^{2}+\mathrm{R} \rho g \mathrm{~h}^{2}+2 \mathrm{RT}\right|$$

Explanation

Pressure is acting on area $$A B C D$$, we have

Pressure Force $$=\int_{0}^{h}\left(\mathrm{P}_{0}+\rho g x\right) \times d x \times 2 \mathrm{R}$$

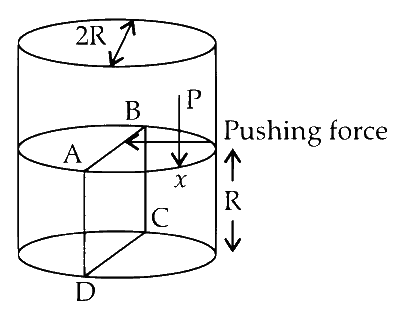
IIT-JEE 2007 Paper 2 Offline Physics - Properties of Matter Question 4 English Explanation

Force due to pressure (push)

$$\begin{aligned}& =\left[\left(\mathrm{P}_{0}+\rho g \frac{x^{2}}{2}\right) 2 \mathrm{R}\right]_{0}^{h} \\\\ & =\left(\mathrm{P}_{0} h+\rho g h^{2} / 2\right) 2 \mathrm{R} \\\\& =2 \mathrm{P}_{0} h \mathrm{R}+\rho g h^{2} \mathrm{R}\end{aligned}$$

Surface tension force (push) $$=T \times 2 R$$

$$\therefore \quad$$ Net Force $$=2 \mathrm{P}_{0} h \mathrm{R}+\rho g h^{2} \mathrm{R}-2 \mathrm{TR}$$

Comments (0)

Advertisement