JEE Advance - Physics (2007 - Paper 2 Offline - No. 4)
A small object of uniform density rolls up a curved surface with an initial velocity $$v$$. It reaches up to a maximum height of $$\frac{3 v^{2}}{4 g}$$ with respect to the initial position. The object is
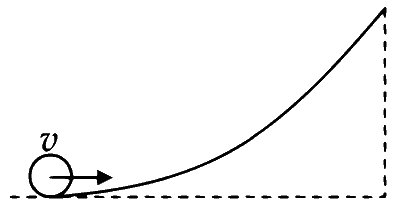
Explanation
By applying conservation of Energy, we have,
$$\frac{1}{2} m v^{2}+\frac{1}{2} \mathrm{I} \omega^{2}=m g h_{\max }$$ ..... (i)
For pure rolling,
$$v=R\omega$$
$$\Rightarrow \quad \omega=v / \mathrm{R}$$ ..... (ii)
Putting eq. (ii) in eq. (i), we get
$$\Rightarrow \frac{1}{2} m v^{2}+\frac{1}{2} \mathrm{I}\left(\frac{v^{2}}{R^{2}}\right)=m g \times \frac{3 v^{2}}{4 g}$$ $$\left(\because h_{\max } \times \frac{3 v^{2}}{4 g}\right)$$
$$\Rightarrow \quad \mathrm{I}=\frac{1}{2} \mathrm{MR}^{2}$$
Hence, this is a required formula of moment of Inertia of Disc. Therefore, the object a disc.
$$2^{\text {nd }}$$ Method : For pure rolling, the velocity of point of contact is zero i.e., $$v=0$$, So, $$\Delta x$$ (displacement) is zero. Then work done by the frictional force should be
$$W=f_{0} \Delta x=0$$
If work is done by dissipative force, work done should be zero. It means that work done of system is zero. So energy should be conserved. Initially, the object has both translation as well as rotational motion. If it attains '$$h_{\max }$$' kinetic energy changes into potential energy.
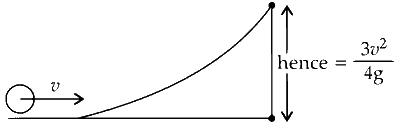
From energy conservation principle,
$$\mathrm{K} . \mathrm{E}_{\text {translational }}+\mathrm{K} . \mathrm{E}_{\text {rotational }}=$$ Potential Energy
$$\Rightarrow \quad \frac{1}{2} m v^{2}+\frac{1}{2} \mathrm{I} \omega^{2}=m g \times \frac{3 v^{2}}{4 g}$$
$$\Rightarrow \quad m v^{2}+\mathrm{I} \omega_{2}=\frac{3 v^{2}}{2} m$$
$$\Rightarrow \quad \mathrm{I} \omega^{2}=\frac{1}{2} m v^{2}$$
$$\Rightarrow \quad \mathrm{I}=\frac{1}{2} \frac{m v^{2}}{\omega^{2}}$$ ..... (i)
For No slipping,
$$\Rightarrow$$ $$\begin{aligned} & v=\omega R \\ & \omega=\frac{v}{R}\end{aligned}$$ ..... (ii)
Put eq (ii) in eq (i)
Hence, $$\quad \mathrm{I}=\frac{1}{2} \mathrm{MR}^{2}$$
$$\mathrm{I}=\frac{1}{2} \mathrm{M} \frac{v^{2}}{v^{2}} \times \mathrm{R}^{2}$$
this is moment of inertia of disc.
So, object is a Disc.
Comments (0)


