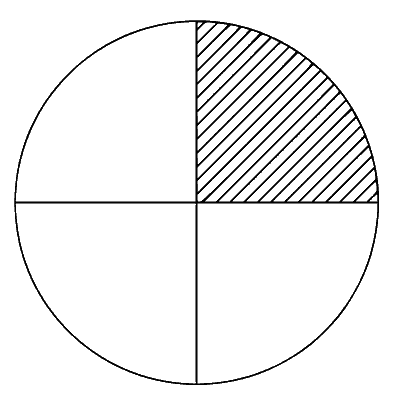
To determine the moment of inertia of a quarter section of a uniform circular disc of radius $R$ and mass $M$ about an axis perpendicular to its plane and passing through the center of the original disc, we start with the moment of inertia of the full disc.

The moment of inertia of a full uniform circular disc about an axis perpendicular to its plane and passing through its center is given by:

$$ I_{\text{full}} = \frac{1}{2} M_{\text{full}} R^2 $$

Since the original disc is uniformly distributed, the mass of the full disc $M_{\text{full}}$ can be split evenly into four equal parts, and mass $M$ corresponds to the quarter section. Hence, we have:

$$ M = \frac{M_{\text{full}}}{4} $$

We also know that the moment of inertia of a quarter section of the disc about the same axis would be one-fourth of that of the entire disc because the mass and area are uniformly distributed. Therefore, the moment of inertia of the quarter section $I_{\text{quarter}}$ is:

$$ I_{\text{quarter}} = \frac{1}{4} I_{\text{full}} $$

Substituting $$ I_{\text{full}} $$ from above:

$$ I_{\text{quarter}} = \frac{1}{4} \left( \frac{1}{2} M_{\text{full}} R^2 \right) $$

Now, replacing $$ M_{\text{full}} $$ with $$ 4M $$ (since $$ M = \frac{M_{\text{full}}}{4} $$), we get:

$$ I_{\text{quarter}} = \frac{1}{4} \left( \frac{1}{2} (4M) R^2 \right) $$

This simplifies to:

$$ I_{\text{quarter}} = \frac{1}{4} \left( 2 M R^2 \right) $$

$$ I_{\text{quarter}} = \frac{1}{2} M R^2 $$

Therefore, the moment of inertia of the quarter section of the disc about the given axis is:

$$ \boxed{ \frac{1}{2} MR^2 } $$

So, the correct answer is Option A: $$ \frac{1}{2} MR^2 $$