JEE Advance - Physics (2000 - No. 1)
A thin wire of length $L$ and uniform linear mass density $\rho$ is bent into a circular loop with centre at $O$ as shown. The moment of inertia of the loop about the axis $XX'$ is:
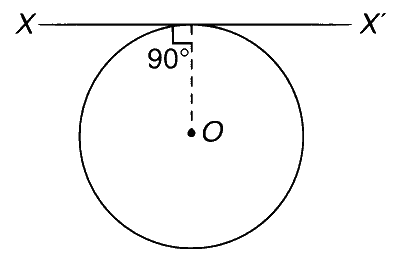
Explanation
Mass of the ring $M=\rho L$. Let $R$ be the radius of the ring, then
$$ L=2 \pi R \quad \text { or } \quad R=\frac{L}{2 \pi} $$
The moment of inertia about an axis passing through the centre $O$ and perpendicular to plane of the loop is $I_z=m R^2$. Using symmetry and perpendicular axis theorem, $I_x+I_y=I_z$, we get
$$ I_x=I_y=\frac{1}{2} I_z=\frac{1}{2} m R^2, $$
where $I_x$ is the moment of inertia about an axis passing through $O$ and lying in the plane of the loop. The centre of mass $O$ of the loop lies at a perpendicular distance $d=R$ from the axis $\mathrm{XX}^{\prime}$. The parallel axis theorem gives
$$ I_{X X^{\prime}}=\frac{1}{2} M R^2+M R^2=\frac{3}{2} M R^2 $$
Substituting values of $M$ and $R$
$$ I_{X X^{\prime}}=\frac{3}{2}(\rho L)\left(\frac{L^2}{4 \pi^2}\right)=\frac{3 \rho L^3}{8 \pi^2} $$
Comments (0)


