Sign In

JEE Advance - Physics (1999 - No. 3)

A particle free to move along the x-axis has potential energy given by $$U\left( x \right) = k\left[ {1 - \exp \left( { - {x^2}} \right)} \right]$$ for $$ - \infty \le x \le - \infty $$, where k is a positive constant of appropriate dimensions. Then
at points away from the origin, the particle is in unstable equilibrium
for any finite nonzero value of x, there is a force directed away from the origin
if its total mechanical energy is $${k \over 2}$$, it has its minimum kinetic energy at the origin
for small displacement from x = 0, the motion is simple harmonic

Explanation

The potential energy $U(x)=k\left[1-e^{-x^2}\right]$, varies with $x$ as shown in the figure.

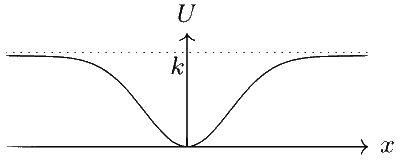
IIT-JEE 1999 Screening Physics - Simple Harmonic Motion Question 24 English Explanation

The potential energy has a local minimum $\left(\frac{\mathrm{d} U}{\mathrm{~d} x}=\right.$ $0, \frac{\mathrm{~d}^2 U}{\mathrm{~d} x^2}>0$ ) at stable equilibrium and local maximum $\left(\frac{\mathrm{d} U}{\mathrm{~d} x}=0, \frac{\mathrm{~d}^2 U}{\mathrm{~d} x^2}<0\right)$ at unstable equilibrium. It is given that potential energy has a stable equilibrium at $x=0$. When particle is displaced from the origin, the force $F=-\mathrm{d} U / \mathrm{d} x$ brings it back. This force points towards the origin. There is no unstable equilibrium.

Total mechanical energy, $U+K=k / 2$, gives kinetic energy of the particle as $K=k / 2-U$, which is maximum at $x=0$. The force on a particle of mass $m$ placed near $x=0$ is given by

$$ \begin{aligned} F & =-\frac{\mathrm{d} U}{\mathrm{~d} x}=-2 k x e^{-x^2}=-2 k x\left(1-\frac{x^2}{2!}+\cdots\right) \\\\ & \approx-2 k x \end{aligned} $$

The force $F$ is proportional to $x$ and points towards $x=$ 0 . Thus, particle executes SHM with angular frequency $\omega=\sqrt{2 k / m}$.

Comments (0)

Advertisement