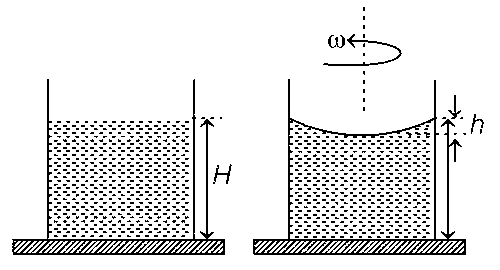
एक बीकर, जिसकी त्रिज्या $$r$$ है, $$H$$ ऊँचाई तक जल से भरा है, जैसा की चित्र में बाईं ओर दर्शाया गया है । जल का अपवर्तनांक (refractive index) $$\frac{4}{3}$$ है | जल से भरा यह बीकर एक क्षैतिज समतल (table) पर रखा गया है । यह निकाय कोणीय गति $$\omega$$ से घूर्णन कर रहा है । इस घूर्णन के कारण जल का पृष्ठ वक्रीय हो जाता है । इससे जल के पृष्ठ के उच्चतम बिंदु (बीकर की परिधि पर स्थित ) एवं न्यूनतम बिंदु (बीकर के अक्ष पर स्थित ) के मध्य की ऊँचाई $$h(h \ll H, h \ll r)$$ हो जाती है जैसा कि चित्र में दायीं ओर दर्शाया गया है । यदि हम इस वक्रीय पृष्ठ को वक्रता त्रिज्या $$R$$ का गोलीय पृष्ठ मानें तो ( $$g$$ गुरुत्वीय त्वरण है )