Sign In

JEE Advance - Mathematics (2025 - Paper 2 Online - No. 8)

Let ℝ denote the set of all real numbers. Let f: ℝ → ℝ be defined by

$f(x) = \begin{cases} \dfrac{6x + \sin x}{2x + \sin x}, & \text{if } x \neq 0, \\ \dfrac{7}{3}, & \text{if } x = 0. \end{cases}$

Then which of the following statements is (are) TRUE?

The point $x = 0$ is a point of local maxima of $f$
The point $x = 0$ is a point of local minima of $f$
Number of points of local maxima of $f$ in the interval $[\pi, 6\pi]$ is 3
Number of points of local minima of $f$ in the interval $[2\pi, 4\pi]$ is 1

Explanation

$$ \begin{aligned} & \lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0^{-}} f(x)=3 \\ & \text { since } 3>\frac{7}{3} \Rightarrow 3>f(0) \end{aligned} $$

$\Rightarrow \mathrm{x}=0$ is local minima ….option (B) is correct

Now,

$$ \begin{aligned} & f(x)=\frac{6 x+\sin x}{2 x+\sin x}=1+\frac{4 x}{2 x+\sin x} \\ & f^{\prime}(x)=\frac{4[(2 x+\sin x) \cdot 1-x(2+\cos x)]}{(2 x+\sin x)^2}=\frac{4(\sin x-x \cos x)}{(2 x+\sin x)^2} \\ & =\frac{4 \cos x(\tan x-x)}{(2 x+\sin x)^2} \end{aligned} $$

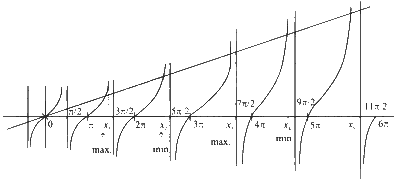
JEE Advanced 2025 Paper 2 Online Mathematics - Application of Derivatives Question 1 English Explanation 1

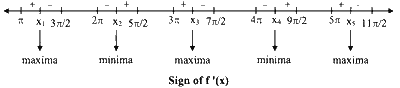
JEE Advanced 2025 Paper 2 Online Mathematics - Application of Derivatives Question 1 English Explanation 2

$$ \text { Options (C) & (D) are also correct. } $$

Comments (0)

Advertisement