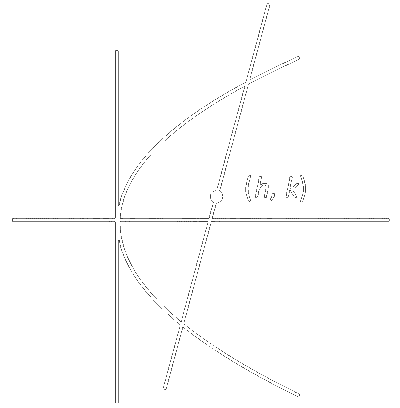
$$ y^2=x $$

chord with given mid point

$$ \begin{aligned} & T=S_1 \\ & y k-\frac{x+h}{2}=k^2-h \\ & 2 k y-x-h=2 k^2-2 h \end{aligned} $$

Now,

$\begin{aligned} & \left.A=\int_{y_1}^{y_2}\left(2 k y-2 k^2+h\right)-y^2\right) d y=\frac{4}{3} \\ & \left(k y^2+\left(h-2 k^2\right) y-\frac{y^3}{3}\right)_{y_1}^{y_2}=\frac{4}{3} \\ & k\left(y_2^2-y_1^2\right)+\left(h-2 k^2\right)\left(y_2-y_1\right)-\frac{1}{3}\left(y_2^3-y_1^3\right)=\frac{4}{3} \\ & \left(y_2-y_1\right)\left[k-2 k+h-2 k^2-\frac{1}{3}\left(4 k^2-2 k^2+h\right)\right]=\frac{4}{3} \\ & 2\left(h-k^2\right)^{1 / 2}\left[2 h-2 k^2\right]=4 \\ & \left(h-k^2\right)^{3 / 2}=1 \\ & x-y^2=1 \Rightarrow y^2=x-1\end{aligned}$

$\begin{aligned} & A=\int_1^4(\sqrt{x}-\sqrt{x-1}) d x \\ & =\frac{2}{3}\left[x^{3 / 2}-(x-1)^{3 / 2}\right]_1^4=\frac{2}{3}[8-3 \sqrt{3}-1] \\ & =\frac{14}{3}-2 \sqrt{3}\end{aligned}$

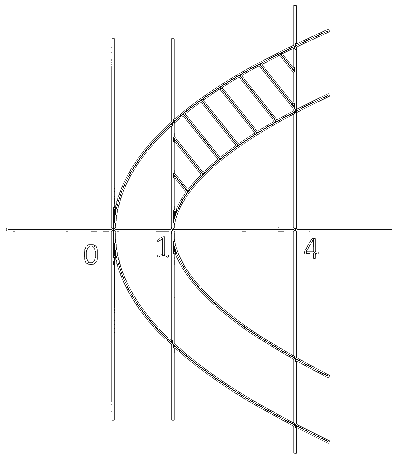
Solving chord and parabola

$$ \begin{aligned} & y k-\frac{y+h}{2}=k^2-h \\ & 2 k y-y^2-h=2 k^2-2 h \\ & y^2-2 k y+2 k^2-h=0 \\ & y_1+y_2=2 k \\ & y_1 y_2=2 k^2-h \\ & y_2-y_1=\sqrt{4 k^2-8 k^2+4 x} \\ & =2 \sqrt{h-k^2} \end{aligned} $$