JEE Advance - Mathematics (2025 - Paper 2 Online - No. 2)
Let ℝ denote the set of all real numbers. Then the area of the region
$ \left\{ (x, y) \in \mathbb{R} \times \mathbb{R} : x > 0, y > \frac{1}{x}, 5x - 4y - 1 > 0, 4x + 4y - 17 < 0 \right\} $
is
$\frac{17}{16} - \log_e{4}$
$\frac{33}{8} - \log_e{4}$
$\frac{57}{8} - \log_e{4}$
$\frac{17}{2} - \log_e{4}$
Explanation
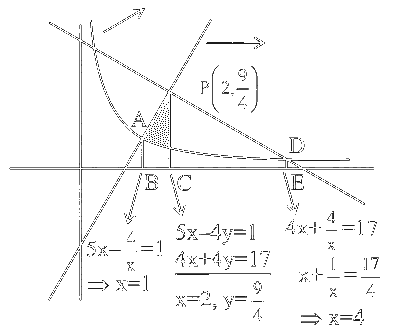
$$ \text { Area }=\underset{\substack{\downarrow \\ \text { Trapezium APBC }}}{\frac{1}{2}\left(1+\frac{9}{4}\right)}+\underset{\substack{\downarrow \\ \text { Trapezium PDCE }}}{\frac{1}{4}\left(\frac{9}{4}+\frac{1}{4}\right)} \cdot 2-\int_1^4 \frac{\mathrm{dx}}{\mathrm{x}} $$
$$ \text { Area }=\frac{13}{8}+\frac{20}{8}-\log _e 4=\left(\frac{33}{8}-\log _e 4\right) $$
Comments (0)


