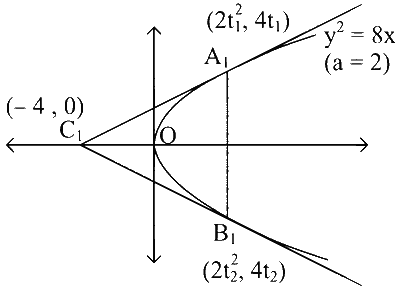
Equation of tangent at (2t$$^2$$, 4t) is

$$\mathrm{ty}=\mathrm{x}+2 \mathrm{t}^2$$

$$\because$$ It is passing through $$(-4,0)$$

$$\therefore 0=-4+2 \mathrm{t}^2 \Rightarrow \mathrm{t}= \pm \sqrt{2}$$

$$\left.\begin{array}{rl} \therefore & \mathrm{A}_1=(4,4 \sqrt{2}) \\ & \mathrm{B}_1=(4,-4 \sqrt{2}) \end{array}\right\} \quad \begin{aligned} & \mathrm{OA}_1=\sqrt{48}=4 \sqrt{3} \\ & \mathrm{~A}_1 \mathrm{~B}_1=8 \sqrt{2} \end{aligned}$$

Equation of altitude of $$\Delta A_1 B_1 C_1$$ drawn from $$A_1$$ is

$$\begin{aligned} & y-4 \sqrt{2}=\sqrt{2}(x-4) \\ & \Rightarrow \sqrt{2} x-y=0 \quad \text{... (1)} \end{aligned}$$

Equation of altitude of $$\Delta A_1 B_1 C_1$$ drawn from $$C_1$$ is

$$\mathrm{x}=0\quad \text{... (2)}$$

Solving (1) and (2) $$\Rightarrow$$ orthocentre is $$(0,0)$$

$$\therefore$$ correct options are (A), (C)