JEE Advance - Mathematics (2024 - Paper 2 Online - No. 6)
A straight line drawn from the point $P(1,3,2)$, parallel to the line $\frac{x-2}{1}=\frac{y-4}{2}=\frac{z-6}{1}$, intersects the plane $L_1: x-y+3 z=6$ at the point $Q$. Another straight line which passes through $Q$ and is perpendicular to the plane $L_1$ intersects the plane $L_2: 2 x-y+z=-4$ at the point $R$. Then which of the following statements is (are) TRUE?
The length of the line segment $P Q$ is $\sqrt{6}$
The coordinates of $R$ are $(1,6,3)$
The centroid of the triangle $P Q R$ is $\left(\frac{4}{3}, \frac{14}{3}, \frac{5}{3}\right)$
The perimeter of the triangle $P Q R$ is $\sqrt{2}+\sqrt{6}+\sqrt{11}$
Explanation
$$\begin{aligned} & \text { line }: \frac{x-1}{1}=\frac{y-3}{2}=\frac{z-2}{1} \\ & (x, y, z)=(\lambda+1,2 \lambda+3, \lambda+2) \\ & \text { Put in } L_1: x-y+3 z=6 \\ & (\lambda+1)-(2 \lambda+3)+3(\lambda+2)=6 \\ & 2 \lambda=2 \Rightarrow \lambda=1 \\ & Q=(2,5,3) \end{aligned}$$
line: $$\frac{x-2}{1}=\frac{y-5}{-1}=\frac{z-3}{3}$$
$$(\mathrm{x}, \mathrm{y}, \mathrm{z})=(\mathrm{t}+2,5-\mathrm{t}, 3 \mathrm{t}+3)$$
Put in $$L_2: 2 x-y+z=-4$$
$$\begin{aligned} & 2(t+4)-(5-t)+(3 t+3)=-4 \\ & 6 t=-6 \Rightarrow t=-1 \\ & R=(1,6,0) \end{aligned}$$
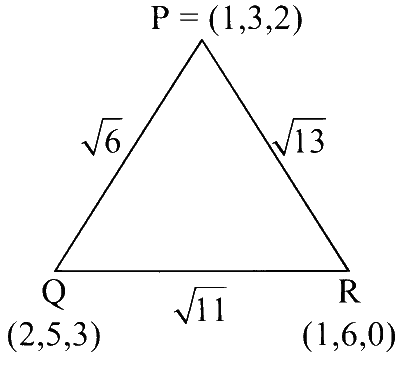
$$\begin{aligned} & \text { Perimeter }=\sqrt{6}+\sqrt{13}+\sqrt{11} \\ & \text { Centroid }=\left(\frac{4}{3}, \frac{14}{3}, \frac{5}{3}\right) \end{aligned}$$
Comments (0)


