JEE Advance - Mathematics (2024 - Paper 2 Online - No. 2)
Let $S=\left\{(x, y) \in \mathbb{R} \times \mathbb{R}: x \geq 0, y \geq 0, y^2 \leq 4 x, y^2 \leq 12-2 x\right.$ and $\left.3 y+\sqrt{8} x \leq 5 \sqrt{8}\right\}$. If the area of the region $S$ is $\alpha \sqrt{2}$, then $\alpha$ is equal to
$\frac{17}{2}$
$\frac{17}{3}$
$\frac{17}{4}$
$\frac{17}{5}$
Explanation
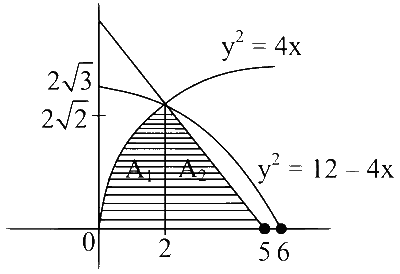
Point of intersection of all curves is $$(2,2 \sqrt{2})$$
$$\begin{aligned} & \text { Area }=\mathrm{A}_1+\mathrm{A}_2 \\ & \alpha \sqrt{2}=\int_\limits0^2 2 \sqrt{\mathrm{x}} \mathrm{dx}+\frac{1}{2} \times 3 \times 2 \sqrt{2} \\ & \alpha \sqrt{2}=2\left[\frac{\mathrm{x}^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^2+3 \sqrt{2} \\ & \alpha \sqrt{2}=\frac{17 \sqrt{2}}{3} \\ & \alpha=\frac{17}{3} \end{aligned}$$
Comments (0)


