Sign In

JEE Advance - Mathematics (2024 - Paper 2 Online - No. 15)

Let $S=\{1,2,3,4,5,6\}$ and $X$ be the set of all relations $R$ from $S$ to $S$ that satisfy both the following properties:

i. $R$ has exactly 6 elements.

ii. For each $(a, b) \in R$, we have $|a-b| \geq 2$.

Let $Y=\{R \in X$ : The range of $R$ has exactly one element $\}$ and $Z=\{R \in X: R$ is a function from $S$ to $S\}$.

Let $n(A)$ denote the number of elements in a set $A$.

Let $S=\{1,2,3,4,5,6\}$ and $X$ be the set of all relations $R$ from $S$ to $S$ that satisfy both the following properties:

i. $R$ has exactly 6 elements.

ii. For each $(a, b) \in R$, we have $|a-b| \geq 2$.

Let $Y=\{R \in X$ : The range of $R$ has exactly one element $\}$ and $Z=\{R \in X: R$ is a function from $S$ to $S\}$.

Let $n(A)$ denote the number of elements in a set $A$.

Let $S=\{1,2,3,4,5,6\}$ and $X$ be the set of all relations $R$ from $S$ to $S$ that satisfy both the following properties:

i. $R$ has exactly 6 elements.

ii. For each $(a, b) \in R$, we have $|a-b| \geq 2$.

Let $Y=\{R \in X$ : The range of $R$ has exactly one element $\}$ and $Z=\{R \in X: R$ is a function from $S$ to $S\}$.

Let $n(A)$ denote the number of elements in a set $A$.

If the value of $n(Y)+n(Z)$ is $k^2$, then $|k|$ is _________.
Answer
36

Explanation

given $$|a-b| \geq 2$$ so if

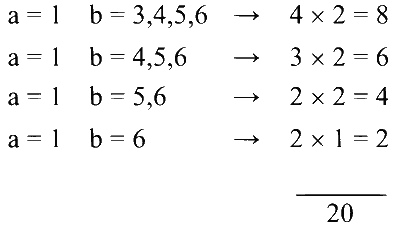
JEE Advanced 2024 Paper 2 Online Mathematics - Permutations and Combinations Question 1 English Explanation

i.e. Total elements in X is $${ }^{20} \mathrm{C}_6$$

Now for $$\mathrm{n}(\mathrm{Y})$$, range of R has exactly one element i.e. second elements must be constant in R and since R must have 6 element so it is not possible to satisfy both condition so $$\mathrm{n}(\mathrm{Y})=0$$.

$$\begin{aligned} \text { for } \quad \mathrm{n}(\mathrm{z}) \quad & 1 \rightarrow 3,4,5,6 \\ & 2 \rightarrow 4,5,6 \\ & 3 \rightarrow 1,5,6 \\ & 4 \rightarrow 1,2,6 \\ & 5 \rightarrow 1,2,3 \\ & 6 \rightarrow 1,2,3,4 \end{aligned}$$

no. of relation that are function will be

$$\begin{aligned} & ={ }^4 \mathrm{C}_1 \times{ }^3 \mathrm{C}_1 \times{ }^3 \mathrm{C}_1 \times{ }^3 \mathrm{C}_1 \times{ }^3 \mathrm{C}_1 \times{ }^4 \mathrm{C}_1 \\ & =(4 \times 3 \times 3)^2=\mathrm{k}^2 \\ & \text { i.e. } \mathrm{k}=36 \end{aligned}$$

Comments (0)

Advertisement