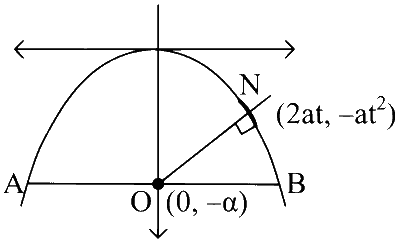
$$\frac{d y}{d x}=\left.\frac{x}{-2 a} \Rightarrow \frac{d y}{d x}\right|_N=-t$$

Slope of normal $$=\frac{1}{t}=\frac{1}{\sqrt{6}} \Rightarrow t=\sqrt{6}$$

Now, $$\frac{-\mathrm{at}^2+\alpha}{2 \mathrm{at}}=\frac{1}{\mathrm{t}}$$

$$\Rightarrow-\mathrm{at}^2+\alpha=2 \mathrm{a}$$

$$\Rightarrow-6 \mathrm{a}+\alpha=2 \mathrm{a} \Rightarrow \alpha=8 \mathrm{a}$$

For A and B

$$\begin{aligned} & x^2=-4 a(-8 a) \\ & \Rightarrow x^2=32 a^2 \Rightarrow x= \pm 4 \sqrt{2} a \\ & \therefore A(-4 \sqrt{2} a,-8 a), B(4 \sqrt{2} a,-8 a) \\ & \therefore A B^2=(8 \sqrt{2} a)^2=128 a^2=s \\ & \therefore \text { Length of } L R=r=4 a \\ & \Rightarrow \frac{r}{s}=\frac{4 a}{128 a^2}=\frac{1}{16} \\ & \therefore 32 a=16 \Rightarrow a=\frac{1}{2} \\ & \therefore 24 a=12 \text { Ans. } \end{aligned}$$