Sign In

JEE Advance - Mathematics (2024 - Paper 1 Online - No. 7)

Let $\mathbb{R}^3$ denote the three-dimensional space. Take two points $P=(1,2,3)$ and $Q=(4,2,7)$. Let $\operatorname{dist}(X, Y)$ denote the distance between two points $X$ and $Y$ in $\mathbb{R}^3$. Let

$$ \begin{gathered} S=\left\{X \in \mathbb{R}^3:(\operatorname{dist}(X, P))^2-(\operatorname{dist}(X, Q))^2=50\right\} \text { and } \\ T=\left\{Y \in \mathbb{R}^3:(\operatorname{dist}(Y, Q))^2-(\operatorname{dist}(Y, P))^2=50\right\} . \end{gathered} $$

Then which of the following statements is (are) TRUE?

There is a triangle whose area is 1 and all of whose vertices are from $S$.
There are two distinct points $L$ and $M$ in $T$ such that each point on the line segment $L M$ is also in $T$.
There are infinitely many rectangles of perimeter 48 , two of whose vertices are from $S$ and the other two vertices are from $T$.
There is a square of perimeter 48 , two of whose vertices are from $S$ and the other two vertices are from $T$.

Explanation

$$\begin{aligned} & \mathrm{S}=\left\{\mathrm{X}:(\mathrm{XP})^2-(\mathrm{XQ})^2=50\right\} \\ & \mathrm{T}=\left\{\mathrm{Y}:(\mathrm{YQ})^2-(\mathrm{YP})^2=50\right\} \end{aligned}$$

for finding $$S \equiv X(x, y, z)$$ and for $$T \equiv Y(x, y, z)$$

$$\begin{aligned} & \left((x-1)^2+(y-1)^2+(z-1)^2\right)-\left((x-4)^2+(y-2)^2+(z-7)^2\right)=50 \\ & \Rightarrow \quad S=\{(x, y, z): 6 x+8 z=105\} \\ & \quad \quad T=\{(x, y, z): 6 x+8 z=5\} \end{aligned}$$

Since S and T both are plane;

(A) There exist a triangle in plane S whose area $$=1$$ (always)

(B) L & M lies on plane T, hence line segment joining L & M will lie on plane T.

(C) Distance between $$\mathrm{S}$$ & $$\mathrm{T}$$

$$\mathrm{d}=\left|\frac{105-5}{10}\right|=10$$

Hence for rectangle of perimeter 48 can exist.

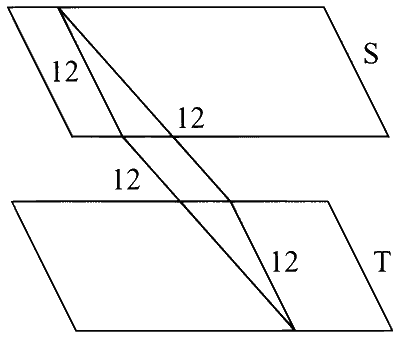
JEE Advanced 2024 Paper 1 Online Mathematics - 3D Geometry Question 3 English Explanation 1

There will be infinite such rectangle possible.

(D) For square

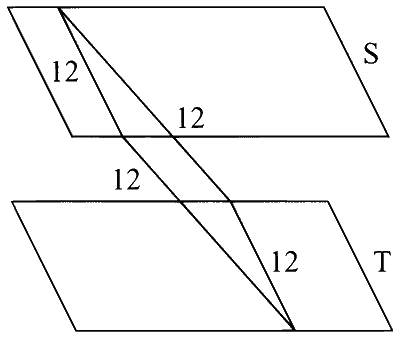
JEE Advanced 2024 Paper 1 Online Mathematics - 3D Geometry Question 3 English Explanation 2

Hence Answers A, B, C, D are correct.

Comments (0)

Advertisement