JEE Advance - Mathematics (2024 - Paper 1 Online - No. 4)
Consider the ellipse $\frac{x^2}{9}+\frac{y^2}{4}=1$. Let $S(p, q)$ be a point in the first quadrant such that $\frac{p^2}{9}+\frac{q^2}{4}>1$. Two tangents are drawn from $S$ to the ellipse, of which one meets the ellipse at one end point of the minor axis and the other meets the ellipse at a point $T$ in the fourth quadrant. Let $R$ be the vertex of the ellipse with positive $x$-coordinate and $O$ be the center of the ellipse. If the area of the triangle $\triangle O R T$ is $\frac{3}{2}$, then which of the following options is correct?
$q=2, p=3 \sqrt{3}$
$q=2, p=4 \sqrt{3}$
$q=1, p=5 \sqrt{3}$
$q=1, p=6 \sqrt{3}$
Explanation
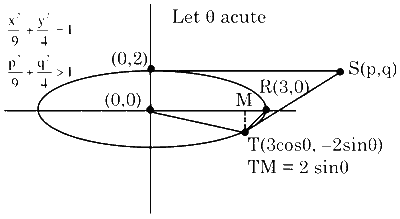
$\operatorname{Ar}(\Delta \mathrm{ORT})=\frac{3}{2}$
$\begin{aligned} & \left|\frac{1}{2} \times 3 \times 2 \sin \theta\right|=\frac{3}{2} \\\\ & \sin \theta=\frac{1}{2} \Rightarrow \theta=\frac{11 \pi}{6} \\\\ & \mathrm{~T}\left(\frac{3 \sqrt{3}}{2},-1\right)\end{aligned}$
Tanget at $(0,2)
$,
$\frac{x(0)}{9}+\frac{y(2)}{4}=1 \Rightarrow y=2$ .........(1)
Tangent at $\left(\frac{3 \sqrt{3}}{2},-1\right) $,
$\frac{x\left(\frac{3 \sqrt{3}}{2}\right)}{9}+\frac{y(-1)}{4}=1$ ...........(2)
$\therefore$ By solving (1) & (2) $\Rightarrow \mathrm{p}=3 \sqrt{3}, \mathrm{q}=2$
$\Rightarrow$ Option $(\mathrm{A})$ is Correct.
Comments (0)


