Sign In

JEE Advance - Mathematics (2024 - Paper 1 Online - No. 17)

Let $f: \mathbb{R} \rightarrow \mathbb{R}$ and $g: \mathbb{R} \rightarrow \mathbb{R}$ be functions defined by

$$ f(x)=\left\{\begin{array}{ll} x|x| \sin \left(\frac{1}{x}\right), & x \neq 0, \\ 0, & x=0, \end{array} \quad \text { and } g(x)= \begin{cases}1-2 x, & 0 \leq x \leq \frac{1}{2}, \\ 0, & \text { otherwise } .\end{cases}\right. $$

Let $a, b, c, d \in \mathbb{R}$. Define the function $h: \mathbb{R} \rightarrow \mathbb{R}$ by

$$ h(x)=a f(x)+b\left(g(x)+g\left(\frac{1}{2}-x\right)\right)+c(x-g(x))+d g(x), x \in \mathbb{R} . $$

Match each entry in List-I to the correct entry in List-II.

List-I List-II
(P) If $a = 0$, $b = 1$, $c = 0$, and $d = 0$, then (1) $h$ is one-one.
(Q) If $a = 1$, $b = 0$, $c = 0$, and $d = 0$, then (2) $h$ is onto.
(R) If $a = 0$, $b = 0$, $c = 1$, and $d = 0$, then (3) $h$ is differentiable on $\mathbb{R}$.
(S) If $a = 0$, $b = 0$, $c = 0$, and $d = 1$, then (4) the range of $h$ is $[0, 1]$.
(5) the range of $h$ is $\{0, 1\}$.

The correct option is
$(\mathrm{P}) \rightarrow(4)$ $(\mathrm{Q}) \rightarrow(3)$ $(\mathrm{R}) \rightarrow(1)$ (S) $\rightarrow$ (2)
$(\mathrm{P}) \rightarrow(5)$ $(\mathrm{Q}) \rightarrow(2)$ $(\mathrm{R}) \rightarrow(4)$ (S) $\rightarrow(3)$
$(\mathrm{P}) \rightarrow(5)$ $(\mathrm{Q}) \rightarrow(3)$ $(\mathrm{R}) \rightarrow(2)$ $(\mathrm{S}) \rightarrow(4)$
$(\mathrm{P}) \rightarrow(4)$ $(\mathrm{Q}) \rightarrow(2)$ $(\mathrm{R}) \rightarrow(1)$ $(\mathrm{S}) \rightarrow(3)$

Explanation

$$f(x)=\left\{\begin{array}{cc} x|x| \sin \frac{1}{x} & ; x \neq 0 \\ 0 & ; \quad x=0 \end{array} \quad g(x)=\left\{\begin{array}{cc} 1-2 x & 0 \leq x \leq \frac{1}{2} \\ 0 ; & \text { otherwise } \end{array}\right.\right.$$

$$g\left(\frac{1}{2}-x\right)=\left\{\begin{array}{cc} 2 x & ; \quad 0 \leq \frac{1}{2}-x \leq \frac{1}{2} \\ 0 ; & \text { otherwise } \end{array}=\left\{\begin{array}{cc} 2 x ; & 0 \leq x \leq \frac{1}{2} \\ 0 ; & \text { otherwise } \end{array}\right\}\right.$$

$$g(x)+g\left(\frac{1}{2}-x\right)=\left\{\begin{array}{ll} 1 ; & 0 \leq x \leq \frac{1}{2} \\ 0 & ; \text { otherwise } \end{array}\right\}$$

(P) $$\quad$$ Now $$a=0, b=1, c=0, d=0$$

$$\because h(x)=g(x)+g\left(\frac{1}{2}-x\right)= \begin{cases}1 ; & 0 \leq x \leq \frac{1}{2} \\ 0 ; & \text { otherwise }\end{cases}$$

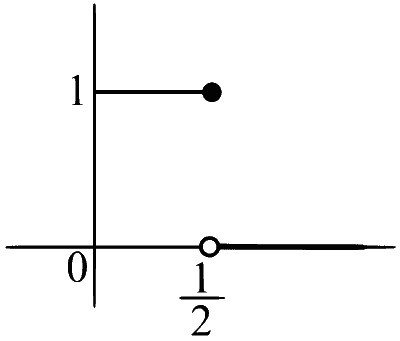
JEE Advanced 2024 Paper 1 Online Mathematics - Limits, Continuity and Differentiability Question 4 English Explanation 1

Hence Range of h(x) is {0, 1}

(Q) $$\mathrm{a}=1, \mathrm{~b}=0, \mathrm{c}=0, \mathrm{~d}=0$$

$$h(x)=f(x)=\left\{\begin{array}{cc} x|x| \sin \frac{1}{x} & ; x \neq 0 \\ 0 & ; x=0 \end{array}\right.$$

$$\begin{aligned} & R H D=\lim _{x \rightarrow 0} \frac{x^2 \sin \frac{1}{x}-0}{x}=0 \\ & \text { LHD }=\lim _{x \rightarrow 0} \frac{-x^2 \sin \frac{1}{x}-0}{x}=0 \end{aligned}$$

Hence $$h(x)$$ is differentiable on $$R$$

(R) $$\mathrm{a}=0, \mathrm{~b}=0, \mathrm{c}=1, \mathrm{~d}=0$$

$$h(x)=x-g(x)=\left\{\begin{array}{cl} 3 x-1 & ; 0 \leq x \leq \frac{1}{2} \\ 0 ; & \text { otherwise } \end{array}\right.$$

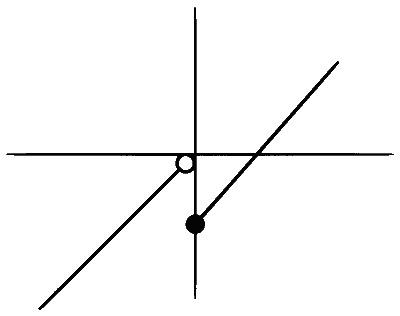
JEE Advanced 2024 Paper 1 Online Mathematics - Limits, Continuity and Differentiability Question 4 English Explanation 2

$$\therefore \mathrm{h}(\mathrm{x}) \text { is ONTO }$$

(S) $$a=0, b=0, c=0, d=1$$

$$h(x)=g(x)=\left\{\begin{array}{cl} 1-2 x & ; 0 \leq x \leq \frac{1}{2} \\ 0 ; & \text { otherwise } \end{array}\right.$$

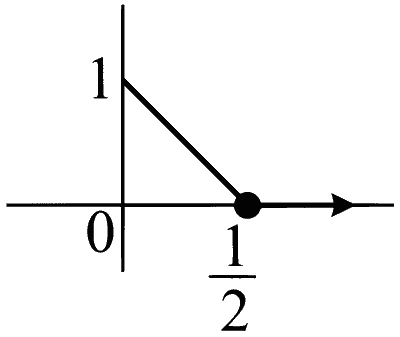
JEE Advanced 2024 Paper 1 Online Mathematics - Limits, Continuity and Differentiability Question 4 English Explanation 3

Range of h(x) is [0, 1]

Comments (0)

Advertisement