Sign In

JEE Advance - Mathematics (2024 - Paper 1 Online - No. 15)

Let the straight line $y=2 x$ touch a circle with center $(0, \alpha), \alpha>0$, and radius $r$ at a point $A_1$. Let $B_1$ be the point on the circle such that the line segment $A_1 B_1$ is a diameter of the circle. Let $\alpha+r=5+\sqrt{5}$.

Match each entry in List-I to the correct entry in List-II.

List-I List-II
(P) $\alpha$ equals (1) $(-2, 4)$
(Q) $r$ equals (2) $\sqrt{5}$
(R) $A_1$ equals (3) $(-2, 6)$
(S) $B_1$ equals (4) $5$
(5) $(2, 4)$

The correct option is
$(\mathrm{P}) \rightarrow(4) \quad(\mathrm{Q}) \rightarrow(2) \quad(\mathrm{R}) \rightarrow(1) \quad(\mathrm{S}) \rightarrow(3)$
$(\mathrm{P}) \rightarrow(2) \quad(\mathrm{Q}) \rightarrow(4) \quad(\mathrm{R}) \rightarrow(1) \quad(\mathrm{S}) \rightarrow(3)$
$(\mathrm{P}) \rightarrow(4) \quad(\mathrm{Q}) \rightarrow(2) \quad(\mathrm{R}) \rightarrow(5) \quad(\mathrm{S}) \rightarrow(3)$
$(\mathrm{P}) \rightarrow(2) \quad(\mathrm{Q}) \rightarrow(4) \quad(\mathrm{R}) \rightarrow(3) \quad(\mathrm{S}) \rightarrow(5)$

Explanation

JEE Advanced 2024 Paper 1 Online Mathematics - Circle Question 1 English Explanation

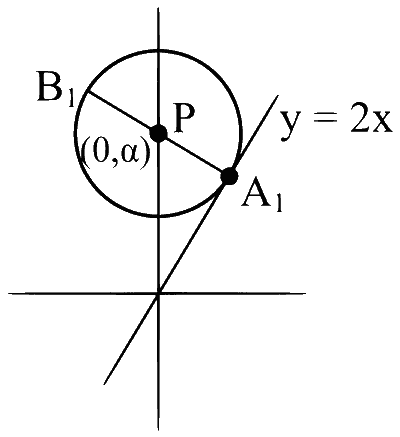
Consider centre as $$\mathrm{P}(0, \alpha), \alpha>0$$

$$\left|\frac{2(0)-\alpha}{\sqrt{5}}\right|=\mathrm{r}$$

$$\begin{aligned} & |-\alpha|=\sqrt{5} r \\ & \alpha=\sqrt{5} r \\ & \therefore \alpha+r=5+\sqrt{5} \\ & \sqrt{5} r+r=\sqrt{5}(\sqrt{5}+1) \\ & r=\sqrt{5}, \alpha=5 \\ & \therefore P(0,5) \end{aligned}$$

Foot of perpendicular from $$P$$ to line $$2 x-y=0$$

$$\begin{aligned} & \frac{x-0}{2}=\frac{y-5}{-1}=\frac{-(2(0)-5)}{5}=1 \\ & x=2, y=4 \quad A_1(2,4) \end{aligned}$$

Let $$\mathrm{B}(\mathrm{p}, \mathrm{q}) \quad \therefore \frac{\mathrm{p}+2}{2}=0, \frac{\mathrm{q}+4}{2}=5$$

$$\therefore \mathrm{p}=-2, \mathrm{q}=6 \quad B(-2,6)$$

Comments (0)

Advertisement