JEE Advance - Mathematics (2023 - Paper 2 Online - No. 8)
For $x \in \mathbb{R}$, let $\tan ^{-1}(x) \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$. Then the minimum value of the function $f: \mathbb{R} \rightarrow \mathbb{R}$ defined by $f(x)=\int\limits_0^{x \tan ^{-1} x} \frac{e^{(t-\cos t)}}{1+t^{2023}} d t$ is :
Answer
0
Explanation
$\begin{aligned} f(x) & =\int\limits_0^{x \tan ^{-1} x} \frac{e^{t-\cos t}}{1+t^{2023}} d t \\\\ f^{\prime}(x) & =\frac{e^{x \tan ^{-1} x-\cos \left(x \tan ^{-1} x\right)}}{1+\left(x \tan ^{-1} x\right)^{2023}}\left(\frac{x}{1-x^2}+\tan ^{-1} x\right)\end{aligned}$
For max/min put $f^{\prime}(x)=0$
$$ \begin{aligned} & \Rightarrow \frac{x}{1+x^2}+\tan ^{-1} x=0 \\\\ & \Rightarrow x=0 \end{aligned} $$
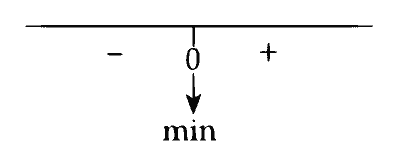
$\therefore f(x)$ has minimum at $x=0$
And $f(x)_{\min }=f(0)=0$
For max/min put $f^{\prime}(x)=0$
$$ \begin{aligned} & \Rightarrow \frac{x}{1+x^2}+\tan ^{-1} x=0 \\\\ & \Rightarrow x=0 \end{aligned} $$

$\therefore f(x)$ has minimum at $x=0$
And $f(x)_{\min }=f(0)=0$
Comments (0)


