JEE Advance - Mathematics (2023 - Paper 2 Online - No. 7)
Let $S$ be the set of all twice differentiable functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that $\frac{d^2 f}{d x^2}(x)>0$ for all $x \in(-1,1)$. For $f \in S$, let $X_f$ be the number of points $x \in(-1,1)$ for which $f(x)=x$. Then which of the following statements is(are) true?
There exists a function $f \in S$ such that $X_f=0$
For every function $f \in S$, we have $X_f \leq 2$
There exists a function $f \in S$ such that $X_f=2$
There does NOT exist any function $f$ in $S$ such that $X_f=1$
Explanation
$S=$ Set of all twice differentiable functions $\mathrm{f}: \mathrm{R} \rightarrow$ R
$$ \frac{\mathrm{d}^2 \mathrm{f}}{\mathrm{dx}^2}>0 \text { in }(-1,1) $$
Graph ' $\mathrm{f}$ ' is Concave upward.
Number of solutions of $f(x)=x \rightarrow x_f$
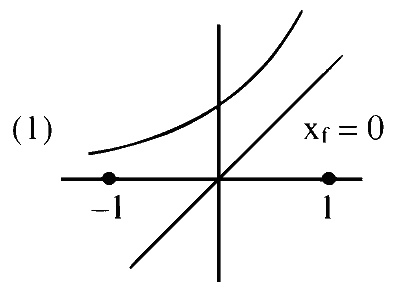
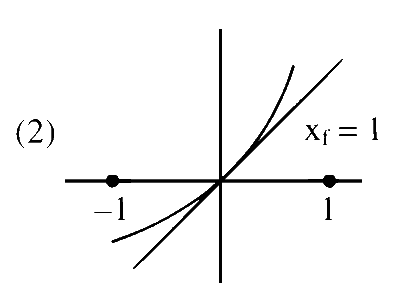
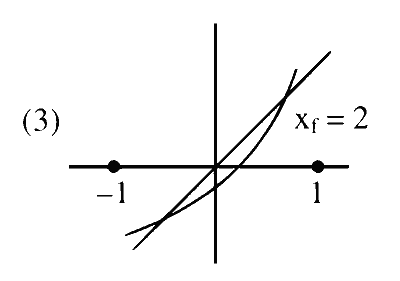
$\Rightarrow$ Graph of $y=f(x)$ can intersect graph of $y=x$ at atmost two points $\Rightarrow 0 \leq x_f \leq 2$
$$ \frac{\mathrm{d}^2 \mathrm{f}}{\mathrm{dx}^2}>0 \text { in }(-1,1) $$
Graph ' $\mathrm{f}$ ' is Concave upward.
Number of solutions of $f(x)=x \rightarrow x_f$
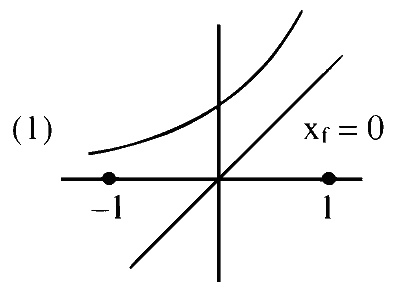
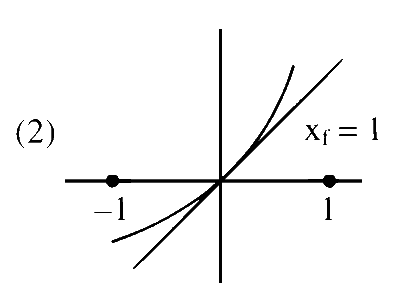

$\Rightarrow$ Graph of $y=f(x)$ can intersect graph of $y=x$ at atmost two points $\Rightarrow 0 \leq x_f \leq 2$
Comments (0)


