JEE Advance - Mathematics (2023 - Paper 2 Online - No. 4)
Let the position vectors of the points $P, Q, R$ and $S$ be $\vec{a}=\hat{i}+2 \hat{j}-5 \hat{k}, \vec{b}=3 \hat{i}+6 \hat{j}+3 \hat{k}$, $\vec{c}=\frac{17}{5} \hat{i}+\frac{16}{5} \hat{j}+7 \hat{k}$ and $\vec{d}=2 \hat{i}+\hat{j}+\hat{k}$, respectively. Then which of the following statements is true?
The points $P, Q, R$ and $S$ are NOT coplanar
$\frac{\vec{b}+2 \vec{d}}{3}$ is the position vector of a point which divides $P R$ internally in the ratio $5: 4$
$\frac{\vec{b}+2 \vec{d}}{3}$ is the position vector of a point which divides $P R$ externally in the ratio $5: 4$
The square of the magnitude of the vector $\vec{b} \times \vec{d}$ is 95
Explanation
$\begin{aligned} & P(\vec{a})=\hat{i}+2 \hat{j}-5 \hat{k} \\\\ & Q(\vec{b})=3 \hat{i}+6 \hat{j}+3 \hat{k} \\\\ & R(\vec{c})=\frac{17}{5} \hat{i}+\frac{16}{5} \hat{j}+7 \hat{k} \\\\ & S(\vec{d})=2 \hat{i}+\hat{j}+\hat{k}\end{aligned}$
From option (A) :
$$ \begin{aligned} & {[\overrightarrow{P Q}, \overrightarrow{P R}, \overrightarrow{P S}] \rightarrow \text { S.T.P }} \\\\ & \left|\begin{array}{ccc} 2 & 4 & 6 \\ \frac{12}{5} & \frac{6}{5} & 12 \\ 1 & -1 & 6 \end{array}\right|=0 \end{aligned} $$
Hence P, Q, R, S are coplanar.
From option (B) :
$\frac{\vec{b}+2 \vec{d}}{3}=\frac{7 i+8 j+5 k}{3}$
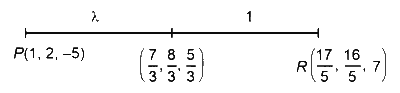
$$ \begin{aligned} & \Rightarrow \frac{\frac{17 \lambda}{5}+1}{1+\lambda}=\frac{7}{3} \\\\ & \Rightarrow \frac{(17 \lambda+5)}{1+\lambda}=\frac{35}{3} \\\\ & \Rightarrow 15 \lambda+15=35+35 \lambda \\\\ & \Rightarrow 16 \lambda=20 \\\\ & \Rightarrow \lambda=\frac{5}{4} \end{aligned} $$
Hence option (B) is correct.
(D)
$\quad \begin{aligned}|\vec{b} \times \vec{d}|^2 & =|\vec{b}|^2|\vec{d}|^2-(\vec{b} \cdot \vec{d})^2 \\\\ & =54 \times 6-225 \\\\ & =324-225 \\\\ & =99\end{aligned}$
From option (A) :

$$ \begin{aligned} & {[\overrightarrow{P Q}, \overrightarrow{P R}, \overrightarrow{P S}] \rightarrow \text { S.T.P }} \\\\ & \left|\begin{array}{ccc} 2 & 4 & 6 \\ \frac{12}{5} & \frac{6}{5} & 12 \\ 1 & -1 & 6 \end{array}\right|=0 \end{aligned} $$
Hence P, Q, R, S are coplanar.
From option (B) :
$\frac{\vec{b}+2 \vec{d}}{3}=\frac{7 i+8 j+5 k}{3}$

$$ \begin{aligned} & \Rightarrow \frac{\frac{17 \lambda}{5}+1}{1+\lambda}=\frac{7}{3} \\\\ & \Rightarrow \frac{(17 \lambda+5)}{1+\lambda}=\frac{35}{3} \\\\ & \Rightarrow 15 \lambda+15=35+35 \lambda \\\\ & \Rightarrow 16 \lambda=20 \\\\ & \Rightarrow \lambda=\frac{5}{4} \end{aligned} $$
Hence option (B) is correct.
(D)
$\quad \begin{aligned}|\vec{b} \times \vec{d}|^2 & =|\vec{b}|^2|\vec{d}|^2-(\vec{b} \cdot \vec{d})^2 \\\\ & =54 \times 6-225 \\\\ & =324-225 \\\\ & =99\end{aligned}$
Comments (0)


