Sign In

JEE Advance - Mathematics (2023 - Paper 2 Online - No. 16)

Consider the $6 \times 6$ square in the figure. Let $A_1, A_2, \ldots, A_{49}$ be the points of intersections (dots in the picture) in some order. We say that $A_i$ and $A_j$ are friends if they are adjacent along a row or along a column. Assume that each point $A_i$ has an equal chance of being chosen.

Consider the $6 \times 6$ square in the figure. Let $A_1, A_2, \ldots, A_{49}$ be the points of intersections (dots in the picture) in some order. We say that $A_i$ and $A_j$ are friends if they are adjacent along a row or along a column. Assume that each point $A_i$ has an equal chance of being chosen.

Consider the $6 \times 6$ square in the figure. Let $A_1, A_2, \ldots, A_{49}$ be the points of intersections (dots in the picture) in some order. We say that $A_i$ and $A_j$ are friends if they are adjacent along a row or along a column. Assume that each point $A_i$ has an equal chance of being chosen.

Let $p_i$ be the probability that a randomly chosen point has $i$ many friends, $i=0,1,2,3,4$. Let $X$ be a random variable such that for $i=0,1,2,3,4$, the probability $P(X=i)=p_i$. Then the value of $7 E(X)$ is :
Answer
24

Explanation

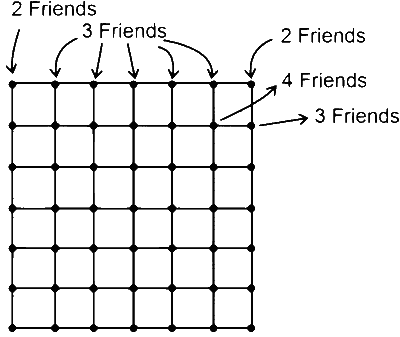
JEE Advanced 2023 Paper 2 Online Mathematics - Probability Question 5 English Explanation
Number of points having 0 friend $=0$

Number of points having 1 friend $=0$

Number of points having 2 friends $=4$

Number of points having 3 friends $=5 \times 4=20$

Number of points having 4 friends $=49-24=25$

$\mathrm{P}_{\mathrm{i}}=$ Probability that randomly selected points has friends

$\mathrm{P}_0=0$ (0 friends)

$\mathrm{P}_1=0$ (exactly 1 friends)

$\mathrm{P}_2=\frac{{ }^4 \mathrm{C}_1}{{ }^{49} \mathrm{C}_1}=\frac{4}{9}$ (exactly 2 friends)

$\mathrm{P}_3=\frac{{ }^{20} \mathrm{C}_1}{{ }^{49} \mathrm{C}_1}=\frac{20}{49}$ (exactly 3 friends)

$\mathrm{P}_4=\frac{{ }^{25} \mathrm{C}_1}{{ }^{49} \mathrm{C}_1}=\frac{25}{49}$ (exactly 4 friends)

$$ \begin{array}{|c|c|c|c|c|c|} \hline x & 0 & 1 & 2 & 3 & 4 \\ \hline P(x) & 0 & 0 & \frac{4}{49} & \frac{20}{49} & \frac{25}{49} \\ \hline \end{array} $$

$\begin{aligned} & \text { Mean }=E(x)=\sum x_i P_i=0+0+\frac{8}{49}+\frac{60}{49}+\frac{100}{49}=\frac{168}{49} \\\\ & 7(E(x))=\frac{168}{49} \times 7=24\end{aligned}$

Comments (0)

Advertisement