JEE Advance - Mathematics (2023 - Paper 2 Online - No. 13)
Let $C_1$ be the circle of radius 1 with center at the origin. Let $C_2$ be the circle of radius $r$ with center at the point $A=(4,1)$, where $1 < r < 3$. Two distinct common tangents $P Q$ and $S T$ of $C_1$ and $C_2$ are drawn. The tangent $P Q$ touches $C_1$ at $P$ and $C_2$ at $Q$. The tangent $S T$ touches $C_1$ at $S$ and $C_2$ at $T$. Mid points of the line segments $P Q$ and $S T$ are joined to form a line which meets the $x$-axis at a point $B$. If $A B=\sqrt{5}$, then the value of $r^2$ is :
Answer
2
Explanation
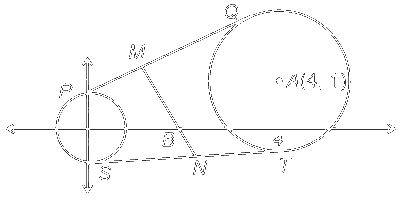
Let $M$ and $N$ be midpoints of $P Q$ and $S T$ respectively.
$\Rightarrow M N$ is a radical axis of two circles
$C_1: x^2+y^2=1$ ........(i)
$\begin{aligned} & C_2:(x-4)^2+(y-1)^2=r^2 \\\\ & \Rightarrow x^2+y^2-8 x-2 y+17-r^2=0 .......(ii)\end{aligned}$
From (i) and (ii);
Equation of $M N: 8 x+2 y-18+r^2=0$
$\Rightarrow B$ is on $x$-axis $\Rightarrow B\left(\frac{18-r^2}{8}, 0\right)$
$$ \begin{aligned} & A B=\sqrt{5} \\\\ & \sqrt{\left(\frac{18-r^2}{8}-4\right)^2+1}=\sqrt{5} \end{aligned} $$
$\Rightarrow$ On solving $r^2=2$
Comments (0)


