$\begin{gathered}R=\left[\begin{array}{lll}a & 3 & b \\ c & 2 & d \\ 0 & 5 & 0\end{array}\right] \\\\ a, b, c, d, \in\{0,3,5,7,11,13,17,19\}\end{gathered}$

Number of invertible matrices $=$ (Total matrices $)-$ (Non Invertible matrices)

$\begin{aligned} & \text { Total matrices }=\begin{array}{cccc}a, & b, & c, & d \\ \downarrow& \downarrow & \downarrow & \downarrow \\ 8 & 8 & 8 & 8\end{array} \\\\ & =8 \times 8 \times 8 \times 8=8^4=4096 \\ & \end{aligned}$

For Non-invertible matrices,

$$ \begin{aligned} & |R|=0 \\\\ & |R|=-5(a d-b c)=0 \end{aligned} $$



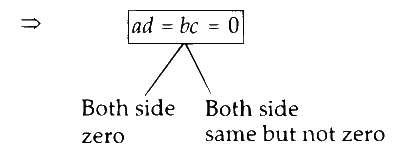
Cases when both side are zero.

(i) All four $a, b, c, d$ are zero.

$$ a d=b c=0 \quad 1 \text { ways } $$

(ii) Three zero and one different digit used for $a, b$, $c, d$.

$$ \Rightarrow a d=b c $$

Select three from four $a, b, c, d$ assign them zero.

$$ \text { i.e., }{ }^4 C_3 \times 1 \times 7=28 \text { ways } $$

(iii) Two zero and two different digits



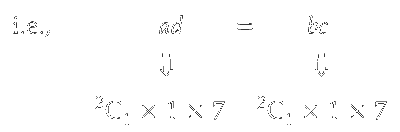
Hence $2 \times 7 \times 2 \times 7=196$ ways

Case II: When both side are same but non zero number.

$$ a d=b c \neq 0 $$

(i) All four $a, b, c, d$ are same.

i.e., $a d=b c$ ( 7 ways)

(ii) Two alike & two alike of another.

$$ a d=b c $$

$$ { }^7 \mathrm{C}_1 \times{ }^6 \mathrm{C}_1 \times 2 !=84 \text { ways } $$

Total number of non invertible matrices are

$$ \begin{aligned} & =1+28+196+7+84 \\\\ & =316 \end{aligned} $$

Hence number of invertible matric

$$ \begin{aligned} & =8^4-316 \\\\ & =3780 \end{aligned} $$