JEE Advance - Mathematics (2023 - Paper 1 Online - No. 9)
Let $n \geq 2$ be a natural number and $f:[0,1] \rightarrow \mathbb{R}$ be the function defined by
$$ f(x)= \begin{cases}n(1-2 n x) & \text { if } 0 \leq x \leq \frac{1}{2 n} \\\\ 2 n(2 n x-1) & \text { if } \frac{1}{2 n} \leq x \leq \frac{3}{4 n} \\\\ 4 n(1-n x) & \text { if } \frac{3}{4 n} \leq x \leq \frac{1}{n} \\\\ \frac{n}{n-1}(n x-1) & \text { if } \frac{1}{n} \leq x \leq 1\end{cases} $$
If $n$ is such that the area of the region bounded by the curves $x=0, x=1, y=0$ and $y=f(x)$ is 4 , then the maximum value of the function $f$ is :
$$ f(x)= \begin{cases}n(1-2 n x) & \text { if } 0 \leq x \leq \frac{1}{2 n} \\\\ 2 n(2 n x-1) & \text { if } \frac{1}{2 n} \leq x \leq \frac{3}{4 n} \\\\ 4 n(1-n x) & \text { if } \frac{3}{4 n} \leq x \leq \frac{1}{n} \\\\ \frac{n}{n-1}(n x-1) & \text { if } \frac{1}{n} \leq x \leq 1\end{cases} $$
If $n$ is such that the area of the region bounded by the curves $x=0, x=1, y=0$ and $y=f(x)$ is 4 , then the maximum value of the function $f$ is :
Answer
8
Explanation
$f(x)$ is decreasing in $\left[0, \frac{1}{2 n}\right]$
increasing in $\left[\frac{1}{2 n}, \frac{3}{4 n}\right]$
decreasing in $\left[\frac{3}{4 n}, \frac{1}{n}\right]$
increasing in $\left[\frac{1}{n}, 1\right]$
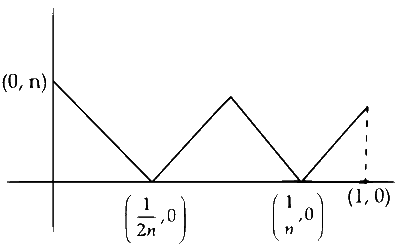
$\begin{aligned} \text { Area } & =\frac{1}{2} \times \frac{1}{2 n} \times n+\frac{1}{2} \times \frac{1}{2 n} \times n+\frac{1}{2} \times\left(1-\frac{1}{n}\right) \times n \\\\ 4 & =\frac{1}{4}+\frac{1}{4}+\frac{n-1}{2} \\\\ 4 & =\frac{1}{2}+\frac{n-1}{2} \\\\ 4 & =\frac{n}{2} \\\\ n & =8\end{aligned}$
increasing in $\left[\frac{1}{2 n}, \frac{3}{4 n}\right]$
decreasing in $\left[\frac{3}{4 n}, \frac{1}{n}\right]$
increasing in $\left[\frac{1}{n}, 1\right]$

$\begin{aligned} \text { Area } & =\frac{1}{2} \times \frac{1}{2 n} \times n+\frac{1}{2} \times \frac{1}{2 n} \times n+\frac{1}{2} \times\left(1-\frac{1}{n}\right) \times n \\\\ 4 & =\frac{1}{4}+\frac{1}{4}+\frac{n-1}{2} \\\\ 4 & =\frac{1}{2}+\frac{n-1}{2} \\\\ 4 & =\frac{n}{2} \\\\ n & =8\end{aligned}$
Comments (0)


