JEE Advance - Mathematics (2023 - Paper 1 Online - No. 5)
Let $Q$ be the cube with the set of vertices $\left\{\left(x_1, x_2, x_3\right) \in \mathbb{R}^3: x_1, x_2, x_3 \in\{0,1\}\right\}$. Let $F$ be the set of all twelve lines containing the diagonals of the six faces of the cube $Q$. Let $S$ be the set of all four lines containing the main diagonals of the cube $Q$; for instance, the line passing through the vertices $(0,0,0)$ and $(1,1,1)$ is in $S$. For lines $\ell_1$ and $\ell_2$, let $d\left(\ell_1, \ell_2\right)$ denote the shortest distance between them. Then the maximum value of $d\left(\ell_1, \ell_2\right)$, as $\ell_1$ varies over $F$ and $\ell_2$ varies over $S$, is :
$\frac{1}{\sqrt{6}}$
$\frac{1}{\sqrt{8}}$
$\frac{1}{\sqrt{3}}$
$\frac{1}{\sqrt{12}}$
Explanation
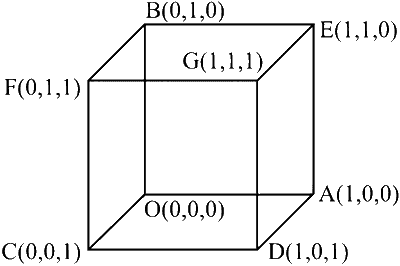
$\mathrm{DR}^{\prime} \mathrm{S}$ of $\mathrm{OG}=1,1,1$
DR'S of AF $=-1,1,1$
DR'S of CE = 1, 1, -1
$\mathrm{DR}^{\prime} \mathrm{S}$ of $\mathrm{BD}=1,-1,1$
Equation of $\mathrm{OG} \Rightarrow \frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{1}=\frac{\mathrm{z}}{1}$
Equation of $\mathrm{AB} \Rightarrow \frac{\mathrm{x}-1}{1}=\frac{\mathrm{y}}{-1}=\frac{\mathrm{z}}{0}$
Normal to both the line's
$$ =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 1 & 1 & 1 \\ 1 & -1 & 0 \end{array}\right|=\hat{i}+\hat{j}-2 \hat{k} $$
$\overrightarrow{\mathrm{OA}}=\hat{\mathrm{i}}$
S.D. $=\frac{|\hat{\mathrm{i}} \cdot(\hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}})|}{|\hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}}|}=\frac{1}{\sqrt{6}}$
Comments (0)


