JEE Advance - Mathematics (2023 - Paper 1 Online - No. 16)
Let $\ell_1$ and $\ell_2$ be the lines $\vec{r}_1=\lambda(\hat{i}+\hat{j}+\hat{k})$ and $\vec{r}_2=(\hat{j}-\hat{k})+\mu(\hat{i}+\hat{k})$, respectively. Let $X$ be the set of all the planes $H$ that contain the line $\ell_1$. For a plane $H$, let $d(H)$ denote the smallest possible distance between the points of $\ell_2$ and $H$. Let $H_0$ be a plane in $X$ for which $d\left(H_0\right)$ is the maximum value of $d(H)$ as $H$ varies over all planes in $X$.
Match each entry in List-I to the correct entries in List-II.
The correct option is:
Match each entry in List-I to the correct entries in List-II.
| List - I | List - II |
|---|---|
| (P) The value of $d\left(H_0\right)$ is | (1) $\sqrt{3}$ |
| (Q) The distance of the point $(0,1,2)$ from $H_0$ is | (2) $\frac{1}{\sqrt{3}}$ |
| (R) The distance of origin from $H_0$ is | (3) 0 |
| (S) The distance of origin from the point of intersection of planes $y=z, x=1$ and $H_0$ is | (4) $\sqrt{2}$ |
| (5) $\frac{1}{\sqrt{2}}$ |
The correct option is:
$$
(P) \rightarrow(2) \quad(Q) \rightarrow(4) \quad(R) \rightarrow(5) \quad(S) \rightarrow(1)
$$
$$
(P) \rightarrow(5) \quad(Q) \rightarrow(4) \quad(R) \rightarrow(3) \quad(S) \rightarrow(1)
$$
$$
(P) \rightarrow(2) \quad(Q) \rightarrow(1) \quad(R) \rightarrow(3) \quad(S) \rightarrow(2)
$$
$$
(P) \rightarrow(5) \quad(Q) \rightarrow(1) \quad(R) \rightarrow(4) \quad(S) \rightarrow(2)
$$
Explanation
$\begin{aligned} & l_1: \vec{r}=\lambda(\hat{i}+\hat{j}+\hat{k}) \\\\ & l_2: \vec{r}=\hat{j}-\hat{k}+\mu(\hat{i}+\hat{k}) \\ & \end{aligned}$
For plane
$d(H)=$ Smallest possible distance between the points of $l_2$ and Plane.
$d\left(H_0\right)=$ Maximum value of $d(H)$
For $d\left(H_0\right)$
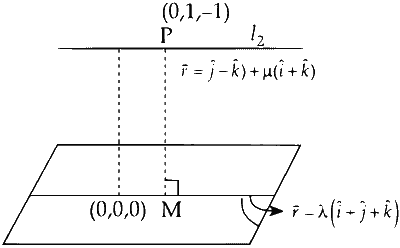
$l_2$ is Parallel to plane containing $l_1$
Equation of plane
$$ a(x)+b y+c z=0 $$
$\because$ It contain $\mathrm{l}_1$
$$ \therefore \mathrm{a}+\mathrm{b}+\mathrm{c}=0 $$ ..........(1)
For largest possible distance between plane (1) and $\mathrm{l}_2$ the line $\mathrm{l}_2$ must be parallel to plane (1)
$$ \therefore \mathrm{a}+\mathrm{c}=0 $$ .........(2)
By (1) and (2) $a=-c, b=0$
$\therefore$ Equation of plane $x-z=0$
(P) $ d\left(H_0\right)=P M=\left|\frac{0-(-1)}{\sqrt{1+1}}\right|=\frac{1}{\sqrt{2}}$
(Q) Distance from $(0,1,2)$
$$ =\left|\frac{0-2}{\sqrt{2}}\right|=\sqrt{2} $$
(R) Distance from origin $(0,0,0)$
$$ =\left|\frac{0}{\sqrt{2}}\right|=0 $$
(S) Point of Intersection,
$$ x-z=0 $$
and
$$ \begin{aligned} & x=1, y=z \\\\ & \therefore x=1=z=y \end{aligned} $$
$\therefore$ Point of intersection $(1,1,1)$ Distance from origin
$$ =\sqrt{1^2+1^2+1^2}=\sqrt{3} $$
For plane
$d(H)=$ Smallest possible distance between the points of $l_2$ and Plane.
$d\left(H_0\right)=$ Maximum value of $d(H)$
For $d\left(H_0\right)$

$l_2$ is Parallel to plane containing $l_1$
Equation of plane
$$ a(x)+b y+c z=0 $$
$\because$ It contain $\mathrm{l}_1$
$$ \therefore \mathrm{a}+\mathrm{b}+\mathrm{c}=0 $$ ..........(1)
For largest possible distance between plane (1) and $\mathrm{l}_2$ the line $\mathrm{l}_2$ must be parallel to plane (1)
$$ \therefore \mathrm{a}+\mathrm{c}=0 $$ .........(2)
By (1) and (2) $a=-c, b=0$
$\therefore$ Equation of plane $x-z=0$
(P) $ d\left(H_0\right)=P M=\left|\frac{0-(-1)}{\sqrt{1+1}}\right|=\frac{1}{\sqrt{2}}$
(Q) Distance from $(0,1,2)$
$$ =\left|\frac{0-2}{\sqrt{2}}\right|=\sqrt{2} $$
(R) Distance from origin $(0,0,0)$
$$ =\left|\frac{0}{\sqrt{2}}\right|=0 $$
(S) Point of Intersection,
$$ x-z=0 $$
and
$$ \begin{aligned} & x=1, y=z \\\\ & \therefore x=1=z=y \end{aligned} $$
$\therefore$ Point of intersection $(1,1,1)$ Distance from origin
$$ =\sqrt{1^2+1^2+1^2}=\sqrt{3} $$
Comments (0)


