$\begin{aligned} & P: \sqrt{3} x+2 y+3 z=16 \\\\ & \qquad S=\left\{\alpha \hat{\imath}+\beta \hat{j}+\gamma \hat{k}: \alpha^2+\beta^2+\gamma^2=1,\right. \left.\quad d_p=\frac{7}{2}\right\} \\\\ & \because|\vec{u}-\vec{v}|=|\vec{v}-\vec{w}|=|\vec{w}-\vec{u}| .............. (1)\end{aligned}$

$\vec{u}, \vec{v}, \vec{w}$ are elements of set $S$ and in set $S$ magnitude of vector is 1

$\therefore \vec{u}, \vec{v}, \vec{w}$ are unit vectors and by equation (1) we can system $\vec{u}, \vec{v}, \vec{w}$ are equally inclined and vertices of equilateral triangle also lying on a circle which is intersection of sphere $|\vec{r}|=1$

Distance from origin to $P$,

$$ d=\frac{|-16|}{\sqrt{3+4+9}}=\frac{16}{4}=4 $$

$\therefore$ Plane containing $\hat{u}, \hat{v}, \hat{w}$ are at a distance

$4-\frac{7}{2}=\frac{1}{2}$ from origin and Parallel to $\sqrt{3 x}+2 y+3 z$ $=16$.

$\therefore$ Equation of the plane is

$$ \begin{array}{rlrl} & \sqrt{3 x}+2 y+3 z & =\gamma \\\\ & \therefore \frac{1}{2} =\left|\frac{\gamma}{4}\right| \\\\ & \Rightarrow \gamma = \pm 2 \\\\ & \sqrt{3 x}+2 y+3 z =2 \end{array} $$

Equation of sphere $x^2+y^2+z^2=1$

$\therefore$ Radius or circle



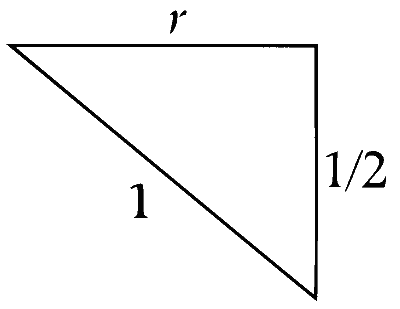
$\begin{aligned} r & =\sqrt{1-\frac{1}{4}}=\frac{\sqrt{3}}{2} \\\\ \text { then } \quad \frac{a}{2} & =\frac{\sqrt{3}}{2} \cos 30^{\circ} \\\\ a & =\sqrt{3} \times \frac{\sqrt{3}}{2}=\frac{3}{2}\end{aligned}$



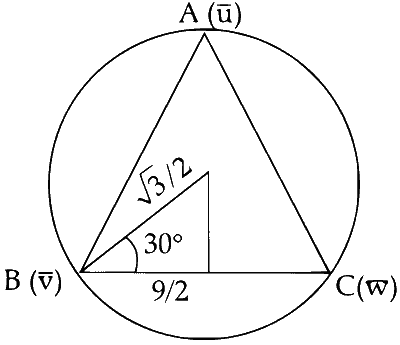
$\therefore$ Area or triangle

$$ =\frac{\sqrt{3}}{2} a^2=\frac{\sqrt{3}}{2} \times \frac{9}{4}=\frac{9 \sqrt{3}}{16} $$

$\therefore$ Volume of Parallelepiped

$$ \begin{aligned} & =2 \times \frac{1}{2} \times \frac{9 \sqrt{3}}{16} \\\\ V & =\frac{9 \sqrt{3}}{16} \end{aligned} $$

$\therefore$ Volume of Parallelepiped

$$ \begin{aligned} = & 2 \times \frac{1}{2} \times \frac{9 \sqrt{3}}{16} \\\\ V & =\frac{9 \sqrt{3}}{16} \end{aligned} $$

$\therefore \frac{80 \mathrm{~V}}{\sqrt{3}}=\frac{80}{\sqrt{3}} \times \frac{9 \sqrt{3}}{16}=45$