JEE Advance - Mathematics (2022 - Paper 2 Online - No. 9)
Let $P Q R S$ be a quadrilateral in a plane, where
$Q R=1, \angle P Q R=\angle Q R S=70^{\circ}, \angle P Q S=15^{\circ}$ and $\angle P R S=40^{\circ}$.
If $\angle R P S=\theta^{\circ}, P Q=\alpha$ and $P S=\beta$, then the interval(s) that contain(s) the value of
$4 \alpha \beta \sin \theta^{\circ}$ is/are
$Q R=1, \angle P Q R=\angle Q R S=70^{\circ}, \angle P Q S=15^{\circ}$ and $\angle P R S=40^{\circ}$.
If $\angle R P S=\theta^{\circ}, P Q=\alpha$ and $P S=\beta$, then the interval(s) that contain(s) the value of
$4 \alpha \beta \sin \theta^{\circ}$ is/are
$(0, \sqrt{2})$
$(1,2)$
$(\sqrt{2}, 3)$
$(2 \sqrt{2}, 3 \sqrt{2})$
Explanation
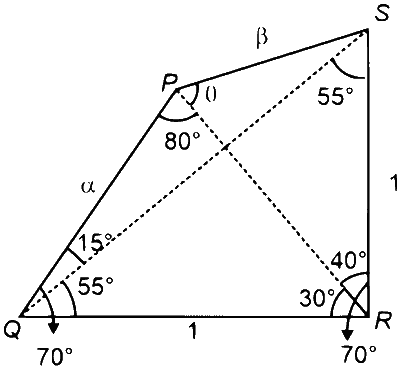
Applying sine rule in $\triangle P Q R$,
$$ \begin{aligned} & \frac{\alpha}{\sin 30^{\circ}}=\frac{1}{\sin 80^{\circ}} \\\\ \Rightarrow & \alpha=\frac{1}{2 \sin 80^{\circ}} \end{aligned} $$
Applying sine rule in $\triangle P R S$,
$$ \begin{aligned} & \frac{\beta}{\sin 40^{\circ}}=\frac{1}{\sin \theta} \\\\ \Rightarrow \beta \sin \theta=& \sin 40^{\circ} \end{aligned} $$
From (i) and (ii),
$$ 4 \alpha \beta \sin \theta=4 \cdot \frac{1}{2 \sin 80^{\circ}} \cdot \sin 40^{\circ}=\frac{1}{\cos 40^{\circ}} $$
Using $\cos 0^{\circ}=1, \cos 30^{\circ}=\frac{\sqrt{3}}{2}, \cos 45^{\circ}=\frac{1}{\sqrt{2}}$ and $\cos 60^{\circ}=\frac{1}{2}$
Only Options (A) and (B) are correct.
Comments (0)


