$$f(x) = {x^2} + {5 \over {12}}$$

This represent upward parabola.

$$g(x) = 2\left( {1 - {{4|x|} \over 3}} \right)$$

At $$x = 0$$

$$g(0) = 2$$

At $$x = {3 \over 4}$$

$$g\left( {{3 \over 4}} \right) = 0$$

$$\therefore$$ Graph is

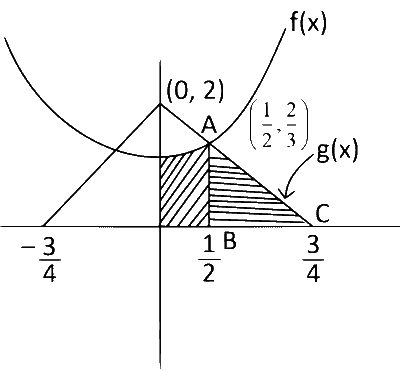
Intersection point of f(x) and g(x) at first quadrant,

$$f(x) = g(x)$$

$$ \Rightarrow {x^2} + {5 \over {12}} = 2\left( {1 - {{4x} \over 3}} \right)$$ [ $$|x| = x$$ as in first quadrant $$x > 0$$ ]

$$ \Rightarrow 12{x^2} + 5 = 24 - 32x$$

$$ \Rightarrow 12{x^2} + 32x - 19 = 0$$

$$ \Rightarrow 12{x^2} + 38x - 6x - 19 = 0$$

$$ \Rightarrow 2x(6x + 19) - 1(6x + 19) = 0$$

$$ \Rightarrow (2x - 1)(6x + 19) = 0$$

$$\therefore$$ $$x = {1 \over 2},\, - {{19} \over 6}$$

In first quadrant $$x = {1 \over 2}$$

When $$x = {1 \over 2}$$,

$$y = {\left( {{1 \over 2}} \right)^2} + {5 \over {12}} = {2 \over 3}$$

$$\therefore$$ Area $$A = 2$$ ( $$\int\limits_0^{{1 \over 2}} {\left( {{x^2} + {5 \over {12}}} \right)dx + } $$ Area of $$\Delta ABC$$ )

$$ = 2\left[ {\int\limits_0^{{1 \over 2}} {\left( {{x^2} + {5 \over {12}}} \right)dx + {1 \over 2} \times \left( {{3 \over 4} - {1 \over 2}} \right) \times {2 \over 3}} } \right]$$

$$ = 2\left[ {\left[ {{{{x^3}} \over 3} + {{5x} \over {12}}} \right]_0^{{1 \over 2}} + {1 \over 2} \times {1 \over 4} \times {2 \over 3}} \right]$$

$$ = 2\left[ {\left( {{1 \over {24}} + {5 \over {12}} \times {1 \over 2}} \right) + {1 \over {12}}} \right]$$

$$ = 2\left[ {{1 \over {24}} + {5 \over {24}} + {2 \over {24}}} \right]$$

$$ = 2\left[ {{{1 + 5 + 2} \over {24}}} \right]$$

$$ = 2 \times {8 \over {24}}$$

$$ = {2 \over 3} = \alpha $$

$$\therefore$$ $$ = 9\alpha = {2 \over 3} \times 9 = 6$$