JEE Advance - Mathematics (2022 - Paper 2 Online - No. 7)
$$ \frac{x^{2}}{100}-\frac{y^{2}}{64}=1 $$
with foci at $S$ and $S_{1}$, where $S$ lies on the positive $x$-axis. Let $P$ be a point on the hyperbola, in the first quadrant. Let $\angle S P S_{1}=\alpha$, with $\alpha<\frac{\pi}{2}$. The straight line passing through the point $S$ and having the same slope as that of the tangent at $P$ to the hyperbola, intersects the straight line $S_{1} P$ at $P_{1}$. Let $\delta$ be the distance of $P$ from the straight line $S P_{1}$, and $\beta=S_{1} P$. Then the greatest integer less than or equal to $\frac{\beta \delta}{9} \sin \frac{\alpha}{2}$ is ________.
Explanation
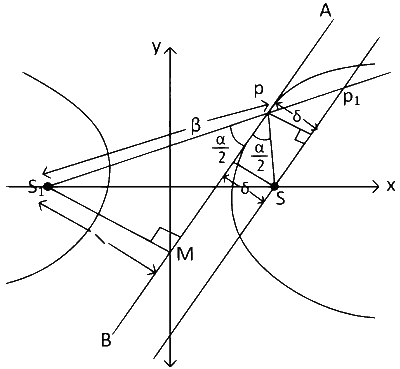
From property we know, tangent and normal is bisector of the angle between focal radii.
$$\therefore$$ Tangent AB divides the angle $$\angle SP{S_1} = \alpha $$ equal parts.
From another property, we know, if we draw perpendicular to the tangent on the hyperbola from two foci, then product of length of the perpendicular from foci = b2
$$\therefore$$ $$l \times \delta = {b^2}$$
Given hyperbola, $${{{x^2}} \over {100}} - {{{y^2}} \over {64}} = 1$$
$$\therefore$$ $${a^2} = 100$$
and $${b^2} = 64$$
$$\therefore$$ $$l \times \delta = 64$$ ....... (1)
From right angle triangle S1 MP we get, $$\sin {\alpha \over 2} = {l \over \beta }$$
$$\therefore$$ $$l = \beta \sin {\alpha \over 2}$$ ....... (2)
Putting value of l in equation (1), we get
$$\left( {\beta \sin {\alpha \over 2}} \right) \times \delta = 64$$
$$ \Rightarrow \delta \beta \sin {\alpha \over 2} = 64$$
$$\therefore$$ $${{\beta \delta } \over 9}\sin {\alpha \over 2}$$
$$ = {{64} \over 9} = 7.1$$
$$\therefore$$ Greatest integer $$ = [7.1] = 7$$
Comments (0)


