JEE Advance - Mathematics (2022 - Paper 2 Online - No. 17)
Suppose that
Box-I contains 8 red, 3 blue and 5 green balls,
Box-II contains 24 red, 9 blue and 15 green balls,
Box-III contains 1 blue, 12 green and 3 yellow balls,
Box-IV contains 10 green, 16 orange and 6 white balls.
A ball is chosen randomly from Box-I; call this ball $b$. If $b$ is red then a ball is chosen randomly from Box-II, if $b$ is blue then a ball is chosen randomly from Box-III, and if $b$ is green then a ball is chosen randomly from Box-IV. The conditional probability of the event 'one of the chosen balls is white' given that the event 'at least one of the chosen balls is green' has happened, is equal to
$\frac{15}{256}$
$\frac{3}{16}$
$\frac{5}{52}$
$\frac{1}{8}$
Explanation
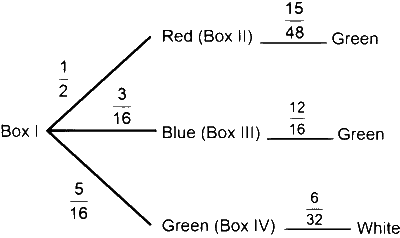
A (one of the chosen ball is white)
B (at least one of the chosen ball is green)
$$ \begin{aligned} P\left(\frac{A}{B}\right) & =\frac{P(A \cap B)}{P(B)} \\\\ & =\frac{\frac{5}{16} \times \frac{6}{32}}{\frac{5}{16} \times 1+\frac{8}{16} \times \frac{15}{48}+\frac{3}{16} \times \frac{12}{16}} \\\\ & =\frac{15}{156}=\frac{5}{52} \end{aligned} $$
Comments (0)


