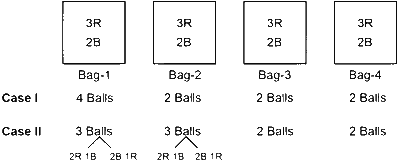
Case 1 :

Among four bags from one bag 4 balls are taken. Number of ways of chosing one bag from 4 bags = $${}^4{C_1}$$

From this bag number of ways of taking 4 balls are

(a) 3 Red and 1 Blue balls, which can be chosen in $${}^3{C_3} \times {}^2{C_1}$$ ways.

(b) 2 Red and 2 Blue balls, which can be chosen in $${}^3{C_2} \times {}^2{C_2}$$ ways.

$$ \therefore $$ Total number of ways of choosing this 4 balls from this bag = $${}^4{C_1}$$$$\left( {{}^3{C_3} \times {}^2{C_1} + {}^3{C_2} \times {}^2{C_2}} \right)$$

Now, two balls are taken from remaining three bags.

From each bag two balls can be taken in $${{}^3{C_1} \times {}^2{C_1}}$$ ways.

So, for three bags two balls can be taken in $${\left( {{}^3{C_1} \times {}^2{C_1}} \right)^3}$$ ways.

$$ \therefore $$ Total number of ways of chosing 10 balls from these four bags

= $${}^4{C_1}$$$$\left( {{}^3{C_3} \times {}^2{C_1} + {}^3{C_2} \times {}^2{C_2}} \right)$$ $$ \times $$ $${\left( {{}^3{C_1} \times {}^2{C_1}} \right)^3}$$

Case 2 :

Among four bags from two bags 3 balls are taken. Number of ways of chosing two bags from 4 bags = $${}^4{C_2}$$

From each bag, number of ways of taking 3 balls are

(a) 2 Red and 1 Blue balls, which can be chosen in $${}^3{C_2} \times {}^2{C_1}$$ ways.

(b) 1 Red and 2 Blue balls, which can be chosen in $${}^3{C_1} \times {}^2{C_2}$$ ways.

So, for two bags three balls can be taken in $${\left( {{}^3{C_2} \times {}^2{C_1} + {}^3{C_1} \times {}^2{C_2}} \right)^2}$$ ways.

$$ \therefore $$ Total number of ways of choosing this 3 balls from this two bags = $${}^4{C_2}$$$${\left( {{}^3{C_2} \times {}^2{C_1} + {}^3{C_1} \times {}^2{C_2}} \right)^2}$$

Now, two balls are taken from remaining two bags.

From each bag two balls can be taken in $${{}^3{C_1} \times {}^2{C_1}}$$ ways.

So, for two bags two balls can be taken in $${\left( {{}^3{C_1} \times {}^2{C_1}} \right)^2}$$ ways.

$$ \therefore $$ Total number of ways of chosing 10 balls from these four bags

= $${}^4{C_2}$$$${\left( {{}^3{C_2} \times {}^2{C_1} + {}^3{C_1} \times {}^2{C_2}} \right)^2}$$ $$ \times $$ $${\left( {{}^3{C_1} \times {}^2{C_1}} \right)^2}$$

From Case 1 and Case 2, total number of ways of chosing 10 balls from these 4 boxes so that from each box at least one red ball and one blue ball are chosen

= $${}^4{C_1}$$$$\left( {{}^3{C_3} \times {}^2{C_1} + {}^3{C_2} \times {}^2{C_2}} \right)$$ $$ \times $$ $${\left( {{}^3{C_1} \times {}^2{C_1}} \right)^3}$$

+ $${}^4{C_2}$$$${\left( {{}^3{C_2} \times {}^2{C_1} + {}^3{C_1} \times {}^2{C_2}} \right)^2}$$ $$ \times $$ $${\left( {{}^3{C_1} \times {}^2{C_1}} \right)^2}$$

$$ \begin{aligned} & =4(5)(6)^3+6(3 \times 2+3)^2(6)^2 \\\\ & =4320+17496 \\\\ & =21816 \end{aligned} $$