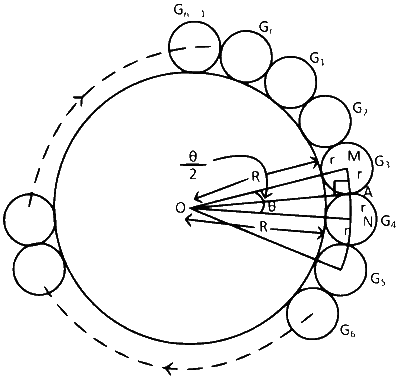
Here if we add center of circles G₁, G₂, G₃ ....... G_n, then we get a polygon of n sides.

From figure you can see one side of polygon makes angle $$\theta$$ with the center.

$$\therefore$$ n sides make angle = n$$\theta$$

We know, $$n\theta = 2\pi $$

$$ \Rightarrow \theta = {{2\pi } \over n}$$

Here triangle OMN is an isosceles triangle. Line joining of point O and midpoint O of MN (point A) is perpendicular to line MN and perpendicular bisector of angle $$\theta$$.

$$\therefore$$ $$\angle MOA = {\theta \over 2} = {\pi \over n}$$

From right angle triangle OMA,

$$\sin {\pi \over n} = {r \over {R + r}}$$

$$ \Rightarrow R + r = r{\mathop{\rm cosec}\nolimits} {\pi \over n}$$

Option A:

When $$n = 4$$,

$$R + r = r{\mathop{\rm cosec}\nolimits} {\pi \over 4}$$

$$ \Rightarrow R + r = \sqrt 2 r$$

$$ \Rightarrow R = \left( {\sqrt 2 - 1} \right)r$$

$$\therefore$$ Option (A) is wrong.

Option B :

When $$n = 5$$,

$$R + r = r{\mathop{\rm cosec}\nolimits} {\pi \over 5} = r{\mathop{\rm cosec}\nolimits} 36^\circ $$

We know, in 0 to $${\pi \over 2}$$, $${\mathop{\rm cosec}\nolimits} \theta $$ is decreasing.

$$\therefore$$ $${\mathop{\rm cosec}\nolimits} 45^\circ < {\mathop{\rm cosec}\nolimits} 36^\circ < {\mathop{\rm cosec}\nolimits} 30^\circ $$

$$ \Rightarrow \sqrt 2 < {\mathop{\rm cosec}\nolimits} 36^\circ < 2$$

$$ \Rightarrow \sqrt 2 r < r{\mathop{\rm cosec}\nolimits} 36^\circ < 2r$$

$$ \Rightarrow \sqrt 2 r - r < r{\mathop{\rm cosec}\nolimits} 36^\circ - r < 2r - r$$

$$ \Rightarrow \left( {\sqrt 2 - 1} \right)r < R < r$$

$$\therefore$$ $$R < r$$, when $$n = 5$$

$$\therefore$$ Option (B) is wrong.

Option C :

When $$n = 8$$,

$$R + r = r{\mathop{\rm cosec}\nolimits} {\pi \over 8}$$

$${\mathop{\rm cosec}\nolimits} \theta$$ is decreasing function in 0 to $${\pi \over 2}$$.

$$\therefore$$ $${\mathop{\rm cosec}\nolimits} {\pi \over 8} > {\mathop{\rm cosec}\nolimits} {\pi \over 4}$$

$$ \Rightarrow r{\mathop{\rm cosec}\nolimits} {\pi \over 8} > \sqrt 2 r$$

$$ \Rightarrow R + r > \sqrt 2 r$$

$$ \Rightarrow R > \left( {\sqrt 2 - 1} \right)r$$

$$\therefore$$ Option (C) is correct.

Option D :

When $$n = 12$$, then

$$R + r = r\left( {\cos ec{\pi \over {12}}} \right)$$

$$ \Rightarrow R + r = r \times {{2\sqrt 2 } \over {\sqrt 3 - 1}}$$ [as $$\cos ec{\pi \over {12}} = {{2\sqrt 2 } \over {\sqrt 3 - 1}}$$]

$$ \Rightarrow R + r = r \times {{2\sqrt 2 \left( {\sqrt 3 + 1} \right)} \over 2}$$

$$ \Rightarrow R + r = \sqrt 2 r\left( {\sqrt 3 + 1} \right)$$

$$ \Rightarrow R = \left[ {\sqrt 2 \left( {\sqrt 3 + 1} \right) - 1} \right]r$$

$$ \Rightarrow R < \sqrt 2 \left( {\sqrt 3 + 1} \right)r$$

$$\therefore$$ Option (D) is correct.